张 晶,夏小刚
数学问题情境化设计中的认知偏差及任务靶向
张 晶1,2,夏小刚1
(1.贵州师范大学 数学科学学院,贵州 贵阳 550001;
2.琼台师范学院 理学院,海南 海口 571127)
在素养时代下,数学问题情境化设计必须解决两个方面的基本问题.一是消除问题情境化设计中的认知偏差,即情境内容选取的偏差、思维方式预设的偏差和问题设计的偏差,从而在问题情境化目标设定与学生认知基础之间形成良好的匹配.二是为了增强问题情境化教学的有效性,需要明确问题情境化设计的任务靶向,创设合适的情境化问题来承载任务靶向,更好地促进学生在知识建构中发展数学素养.
数学问题;
问题情境化;
认知偏差;
任务靶向
当前,中国基础教育正迈向核心素养的新时代.《义务教育数学课程标准(2022年版)》提出素养本位下教师应帮助学生“体会数学知识之间、数学与其它学科之间、数学与生活之间的联系,在探索真实情境所蕴含的关系中,发现问题和提出问题,运用数学和其它学科的知识与方法分析问题和解决问题”的课程目标[1].可见,问题与情境成为发展学生核心素养的重要载体,影响着学生的知识建构和思维发展.为此,需要教师对数学问题的情境化设计形成良好的认知.然而,受知识观以及教学实践诸多因素的影响和制约,教师对问题情境化设计中情境内容的选取、思维方式的预设及问题设计等方面的认识出现失真,形成了一些有失偏颇或有所缺漏的认知,制约了学生数学认知的发展.为了尽可能减少这种现象的发生,必须在问题情境化设计层面加以防范.
数学问题的情境化设计主要指教师基于数学教学的目标指向,结合学生的认知特点,用能体现学生现实的数学语言对数学问题进行重构或重述,以此将数学问题置于与学生现实相关的背景中.这种重构或重述,意味着数学问题在学生面前以可以认识、理解和情感反应的方式表达出来,其目的在于激发学生的认知需求,引发学生的情感体验,增强学生探究问题的针对性和有效性[2].由此形成的情境化问题在结构上具有了整合性特点,即包含了背景、问题、任务以及目的等结构要素,其中,“背景”主要涉及生活的、经验的、知识的相关信息,“问题”则指的是蕴含在情境中的数学问题.譬如,在“不等式”概念教学中,教师设计了如下情境化问题:一辆匀速行驶的列车在10:35距离M地150 km,要在11:05之前驶过M地,车速应该满足什么条件?此问题中,列车行驶是“背景”,车速是多少是“问题”,根据要求求出车速是“任务”,理解不等式概念的含义是“目的”.
关于情境化问题的本质认识,研究者提出了一些具有共性的看法[3–8],主要涉及以下5个方面的认识视角.一是基于数学的现实存在和意义;
二是基于数学知识的认识和理解;
三是基于学生数学兴趣的激发;
四是基于学生问题意识的发展;
五是基于学生数学思维的发展.上述5个维度中,前两个维度与情境化问题的知识层面的认知发展有关,后3个维度更多与学生思维层面的素养发展相关.因此,问题的情境化设计必须在素养的目标指向和学生已有知识与经验之间形成较高的契合,否则,学生在知识理解、知识迁移与知识创生中的素养发展会受到制约.为了减少和避免这种现象的产生,在问题情境化设计中需要解决认知上的价值共识问题.
早期,人们对情境化问题的关注大多来自教育心理学和学科教学研究领域.近20年来,情境化问题进入数学课堂,成为课堂教学的“常客”.按理说,教师对问题情境化设计已非常熟悉,然而,近些年来对一线教师的课堂观察和研究发现,部分教师对问题情境化设计的认识并未深入.或许,由于经世致用的数学自古以来就被看作是学校启蒙教育中一个不可缺少的内容,加上近百年来对知识特别是科学知识的普遍认同,人们在问题情境化设计的知识层面上,形成了有较高契合度的共同认识,即情境化问题对于数学知识的理解和应用是有益的.相比之下,对问题情境化设计的价值认识各有不同,由此形成的认知偏差,导致教师对问题情境化设计中的任务靶向认识模糊,甚至偏离学生核心素养的发展目标.
偏差1 情境内容的选择:重自然属性,轻教学加工
面对核心素养的价值诉求,问题情境化设计必须思考的一个教学问题,就是问题情境化的目的在于帮助学生解决生活世界中的真实情境,以获得更多实践性知识和技能,还是为了运用数学的知识,使学生在教师建构的问题情境中获得知识能力的发展,抑或是两者兼而有之?对这个问题的回答,反映了教师在问题情境化认知上的价值取向,也从中折射出情境化问题的两种基本属性——自然属性和建构特征,其中,“自然属性”主要强调的是情境的“客观性”与“真实性”,其内容主要反映的是自然界与人类生活实践中的规律与现象.对此,比利时教育家罗日叶在其《为了整合学业获得:情境的设计和开发》一书中指出:这是一类建立在真实需要基础上的、需要学生实际解决和完成的自然情境,但是这类情境赖以存在的需要不是为了学习的目的[9].而“建构特征”则强调情境化的教学加工,即通过联系学生的经验世界,将数学问题置于数学知识发生发展的经验性情境中,使之成为具有触发学生思维、引发学生探究功能的“召唤”结构.经验是实践基础上的感知与认识.立足于学生的生活经验,帮助学生积累数学的活动经验,发展数学的思维经验,是情境化设计的应有之义.然而,生活经验具有不同于活动经验与思维经验的特点,蕴含了学生现实生活中的“熟知点”和“兴趣点”.由此,人们形成了这样的认识,即数学学习更容易受到来自学生生活经验的启发.基于这样的认识,教师在问题的情境化设计时,大多习惯联系学生的生活经验,或者通过模仿现实生活来设计情境化问题.但是,随之而来的问题是,教师在“联系”与“模仿”中常常忽略生活的基本常识和行为逻辑,使问题情境成为没有意义的虚拟式场景.
譬如,在“比例尺”教学中,有教师创设了这样的生活情境:你们去过成都吗?重庆到成都的高速列车坐过吗?高速列车美观、舒适、速度快.现在从重庆到成都只需102分,比以前的普通列车快很多.可是,有只蚂蚁只用6秒就从重庆到达了成都,可真厉害了!你知道是为什么吗?这是一个有生活气息的情境化问题,其设计意在通过蚂蚁的“厉害”,激发学生兴趣,帮助学生认识和理解比例尺.然而,蚂蚁真的“厉害”吗?要知道,“102分”指的是高速列车在行驶中从重庆到成都所花的时间,而“6秒”则是蚂蚁从地图上的“重庆”爬行到“成都”所用的时间.可见,“蚂蚁真的厉害”的内容表述既不符合学生经验世界中的基本常识,也不利于学生认识和理解“比例尺”问题的数学本质及其生活意义.
偏差2 思维方式的预设:重横向数学化,轻纵向数学化
问题情境化设计是一种教学预设活动.“预设”指向素养目标的心理预期,意味着教师对情境化问题所承载的素养培育功能的教学规划与安排.素养的核心是思维.学生思维的发展不仅具有生成性,而且离不开教师的精心预设.换言之,思维发展体现了预设与生成的和谐统一.为此,通过教学加工将数学思想方法蕴藏于情境化问题之中,以此把数学问题的思想方法转化为学生可以展开的数学化思维方式,成为问题情境化设计中需要认识和把握的价值意蕴.
“数学化”作为一种数学教学思想,最早是由弗赖登塔尔提出来的,意指“人们在观察、认识和改造客观世界的过程中,运用数学的思想和方法来分析和研究客观世界的种种现象并加以整理和组织的过程”[10].这是一个从现实生活逐渐抽象和形式化的思维过程.然而,从教学的现实图景来看,教师对现实问题数学化的关注,远胜于对数学本身的数学化的思考.具体到问题的情境化设计中,就是过于强调数学与现实生活的联系,注重将横向数学化(经验归纳)的思维方式预设于情境化问题中.无疑,这种情境化设计有利于学生数学思维的预设性发展,即从现实问题的数学思考中抽象出数学知识,或者寻找、解释数学知识在现实中的意义.然而,横向数学化只是数学化的初级阶段,过分和不恰当地强调指向现实生活的情境化,忽视来自数学自身的情境化,这会导致数学教学的“去数学化”.事实上,在教学时数相对稳定的情况下,过多地关注数学问题的“现实生活化”,必然使学生的数学化思考过多停留在拟经验的数学活动中,难以进入较高层次的数学思维发展阶段.
以“平行四边形的性质”教学案例为例.有教师以“折纸活动”为切入点,要求学生将一张纸对折,剪下两个叠放的三角形纸片,并按长度相等的对边重合的要求,拼接四边形.问:有几种拼接四边形的方法?拼图中有平行四边形吗?如果有,请说明理由.然后,教师将学生拼接的图形通过投影仪展示,同时设问:哪些拼图属于平行四边形?试归类,并说明它们有何共性.以此引导学生抽象概括出平行四边形的定义.其设计的目的,意在帮助学生通过“剪纸—拼图—展示—观察—归纳”的探究活动抽象概括出平行四边形定义.显然,其预设的横向数学化方法,为学生实现由生活经验向数学认知的发展提供了有利的条件.
然而,在平行四边形概念问题的情境化设计中,教师对如何将学生的思维从生活引向数学并未给予足够的关注.事实上,作为平行四边形定义的数学化对象,无论是剪纸拼图问题,还是拼图展示问题,它们并未脱离学生的现实生活背景.数学源于生活,但高于生活.作为对此问题的一种改进和思考,教师可以将四边形拼图抽象为四边形图形,将投影中展示的四边形拼图问题转化为有关四边形图形的探究问题,这不仅在四边形图形(而不是拼图)的观察与探究中预设了纵向数学化的思想方法,而且渗透了让学生通过思维去认识和把握数学对象的教学思想.
偏差3 数学问题的设计:重难易度,轻层级性
思维是素养的核心,思维进阶依赖于情境化问题的探索与解决.无疑,关注学生在问题解决中的思维表现,把握问题的难易度和层级性,成为问题情境化设计的基本要求.

应该说,教师对问题情境化设计的教学意义——促进学生知识建构和思维发展已形成基本共识.然而,囿于对情境的信息来源和问题难易度的认识不足,加上缺少对学生数学认知现状的了解,教师在数学问题的情境化设计中,常常过于关注问题的逻辑性与难易度的转化,轻视或有意规避情境化问题的层级性.譬如,在初中教学中,为了引入函数概念,有教师创设了这样一个情境:一架飞机起飞时油箱内的油量为13 t,飞行时每分钟耗油0.12 t,问:油箱内的剩余油量是怎样受到飞行时间的影响和制约的?这是一个典型的情境化问题,其中,飞行和油量的背景信息反映了学生的生活经验,而剩余油量和飞行时间之间具有的内在关系,反映了函数概念的本质——变量之间的依赖关系.然而,对于剩余油量与飞行时间之间的关系问题,教师未就如何从多个关系中引导学生理解和把握给予必要的关注.事实上,在学生思考这个问题之前,可以增设一组结构层次相对低的情境化问题,譬如给出一组具体的飞行时间,让学生回答与每一个飞行时间相对应的剩余油量.这样,情境化问题不仅体现了分层的设计思想,而且为学生在函数关系认识中的思维表现提供了针对性的前提和条件.

图1 情境化问题的层级关系
可见,弥合认知偏差的关键,在于教师应对自身的认知局限保持敏感,避免陷入“自我感知良好”的尴尬.其重要突破口就在于教师应增强自身对问题情境化设计的教学认识,即以深化知识、发展思维为本,以数学认知与学习情感的交融为切入点,以情境化与数学化的关系均衡为尺度,对数学问题进行多层次和多水平的情境化设计.
问题与情境是核心素养的落地之路.实现核心素养由课程目标向教学现实的有效转化,不仅要弥合影响问题情境化设计的认知差异,而且要精心创设承载素养培育功能的情境化问题.
无疑,问题情境化设计的核心就是如何明确问题情境化设计中的任务靶向.然而,美国匹兹堡大学“QUASAR计划”的研究表明,“并非所有的任务类型都有相同的结果,即不同的任务要求学生有不同层次和不同类型的思维,反之,不同层次和不同类型的思维或能力也需要不同的任务来培养”[12].因此,问题情境化设计必须在学生数学活动的聚焦中,明确任务靶向,即结合课程标准的要求、教学内容的理解以及学生的认知基础与诉求,通过情境化的教学加工,将数学问题转化为具有思考性、探究性与层次性的数学任务,以便在“内容之知”的数学探究中,培育学生的“方法之知”——数学的学习方式与思维方式.为此,可以把问题情境化设计中的任务靶向分为两个基本层面:一是学生新知学习能力的发展,二是学生综合能力的发展.在明确了任务靶向的层次性之后,靶向任务的载体就自然落在了靶向式情境问题上.结合罗日叶关于“靶向情境”的内涵界定[9],根据问题情境化教学加工程度不同,可以将情境化问题分为以下3种类型(见图2).
自然形态的情境问题——缺少教学加工,且外在于学生学习环境的情境化问题.
新知学习型情境问题——基于概念、原理、公式、法则等新知教学需要所设计的情境化问题.
综合探究型情境问题——基于综合能力发展需要所设计的情境化问题.

图2 基于任务靶向的情境化问题
其中,新知学习型情境问题、综合探究型情境是值得关注的两类靶向式情境问题.
为了搭建指向素养发展的数学活动平台,解决学生基于知识内化和思维提升的问题,靶向式情境问题设计必须遵循“经验性”原则、“整合性”原则与“适切性”原则,其中“经验性”原则是前提,“整合性”原则是核心,“适切性”原则是关键(关系图见图3).
(1)“经验性”原则.
经验是学习的基础,也是进一步学习的重要资源.早在《民主主义与教育》一书中,杜威就指出:教育即经验的不断改造.然而,在数学教学活动中,学生的经验世界常常被教师排斥与抛弃,导致学习意义的缺失.因此,靶向式情境问题的设计,必须基于学生的经验世界,把学生的生活经验、活动经验和思维经验作为情境化问题对接学习体验的切入口,并将数学问题通过经验性情境进行教学加工,以此形成的数学情境化问题,才能成为数学思维的刺激物,引发有意义的数学学习才有可能.
在此意义下,情境化问题具有了“真实性”.这种“真实性”不是对现实生活的简单模拟,而是通过教师的教学加工,使数学问题指向了学生的经验世界,体现了学生经验世界中的“日常逻辑”.譬如,有这样一个问题:“2022年有365天,有多少个星期?还多几天?”在有余数的除法教学中,这是一个新知学习型情境问题.不过,如果该问题只是现实生活中的问题,且结果只用于生活中的实际需要,那么它就只能是一个自然形态的情境问题.显然,这两种形态的问题都不违“日常逻辑”,它们都具有“真实性”.但是,两者的价值指向却各有不同,前者是对有余数的除法问题“365÷7=?”的生活情境化,其问题的解决蕴含了数学化的思想与方法,而后者只是出于生活环境的需要,不具有教学上的意义和价值.
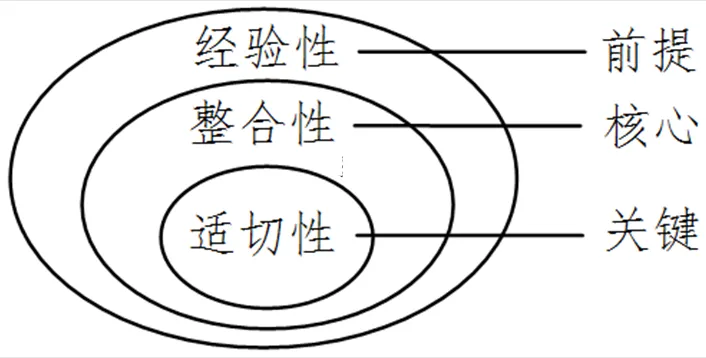
图3 靶向式情境问题设计原则关系
可见,设计靶向式情境问题的前提,在于能否通过对接学生的经验世界,遵循经验世界的“日常逻辑”,还原知识的经验性内容,将数学问题嵌入到学生可以感知的经验性情境之中,从而使情境化问题的价值指向能够在经验性内容的“召唤”中被激发和显现.
(2)“整合性”原则.
情境与问题是教学与思维的核心要素,正如杜威在《民主主义与教育》中指出的:“教学法的要素和思维的要素是相同的.这些要素是:第一,学生要有一个真实的经验的情境——要有一个对活动本身感到兴趣的连续的活动;
第二,在这个情境内部产生一个真实的问题,作为思维的刺激物……”[13]由于素养源自情境问题中的思维张力,思维来自情境任务中的问题探索,因此,将问题与情境“整合”,使思维的张力转化为均衡的数学化任务,并且置于学生的经验世界之中,这成为问题情境化设计的基本要求.这里,“整合”的方式有两种:一种方式是将问题中的概念及关系要素组织到经验性情境中,同时指向横向数学化的思维方式.以此构建的情境化学习任务,体现的是问题与情境的“横向”加工方式.与此相对应的“纵向”加工方式,就是将蕴含在情境化问题中的数学任务分解为一组子情境任务,使这组子任务不仅体现融入这个情境任务讨论的自然过程,而且指向纵向数学化的思维过程.
以“勾股定理”为例.勾股定理是平面几何的一个基本定理,为了揭示直角三角形中蕴含的数形关系,即一个直角的“形”的特点决定了三边之间的“数”的关系,有教师设计了如下情境化问题:如图4所示的方格纸上分别呈现了4个直角三角形,请你在表格(略)中完成有关2、2、2的数值填写,看看能从中发现直角边、与斜边之间有什么数量关系.

图4 方格上的直角三角形
学生通过操作、计算、观察,然后归纳表格中的数量关系,可以发现4个直角三角形中两直角边与斜边之间的数量关系:2+2=2.在此基础上,教师继续设问:这种直角边与斜边之间数量关系对于一般直角三角形是否成立?这种情境化设计,有助于在探究中暴露学生已有的知识经验,进而促进数学化思维的发展.
数学素养是“学生在今后的生活、学习和工作中所需要的数学知识与技能”(PISA),因此,整合情境化问题中的知识与技能,成为靶向式情境问题的设计的核心.为此,需要教师在“整合”中进一步优化情境素材以及数学的关系和结构,以唤醒学生的生活经验、活动经验和思维经验,进而调动更多的知识、技能与态度.
(3)“适切性”原则.
“适切性”意指问题情境化设计中情境诸要素与数学的关系和结构之间形成的相关性,表现为合适、恰当、适应等方面特征.换言之,面对培育学生核心素养的时代要求,问题情境化设计不仅要契合教学目标的要求,而且要与知识本质的理解、学生的认知基础相匹配.其核心要义就是,根据教学任务的需要,将情境化问题的难易度保持在合理水平.无疑,情境化问题的基本构成决定了影响其难易度的两个基本因素——表征背景的复杂度和去背景问题的难易度,“表征背景中关系的复杂程度,反映了从背景问题中抽象出无背景问题的难易”[14],而“去背景问题”的难易度与问题表征的关系密切.事实上,Ktovsky等研究者在对中国益智游戏——九连环的研究中发现,“问题难度的来源之一就是对于如何操作的发现过程,因为他们发现,信息程度提示高的变式比较容易解决,反之,则不易解决”[15].国内也有类似的研究结论,即“给背景问题加入合适的提示后,会降低问题解决的难度,并且提示的作用在中等难度的背景问题中最为明显”[14].因此,在问题情境化设计中,可以通过以下方式,赋予情境化问题所需要的难度水平:第一,强化(或弱化)背景表征的复杂性以及背景所涉及的知识基础;
第二,增加(或减少)去背景问题的信息提示.其教学加工的强弱程度,取决于情境任务的靶向需求和学生已有的知识与经验.如在“探索相似三角形的条件”教学中,有教师设计了这样的情境化问题:与同伴合作,两个人分别画△和△,使得∠=∠=30°,∠=∠=45°,此时,这样的两个三角形相似吗?说说理由.为了增强问题的数学特征,教师改变了问题中的数学信息,即将“30°”“45°”分别改为给定的“∠”“∠”(0°<∠,∠<90°),这样,学生要判断△和△是否相似,就得考虑“∠”和“∠”的任意性及由此产生的归纳推理.进一步地,教师对问题的背景信息进行改变,将“画图”改为了“几何画板演示”,由此得到一个新的情境化问题:(用几何画板演示)改变角的大小,但是始终保持∠=∠、∠=∠,观察 △和△是否相似?无疑,这增强了三角形相似判定的视觉特征,也同时增加了三角形相似判定的信息提示.尽管在一定程度上降低了情境化问题的难度水平,但是对于学生在理解和掌握相似三角形判定方法中,提高分析问题、解决问题的能力具有积极意义.
问题情境化对学生数学素养的发展具有重要影响.基于学生的经验世界,将数学问题与背景信息进行整合,使情境化问题不仅契合教学目标的要求,而且促进学生在理解知识本质的同时,发展数学素养,这成为教育新时代的教学主旋律.因此,对于问题情境化设计必须在认知上进行深化和引导,同时增强问题情境化教学的有效性.为此,数学教学中的问题情境化设计必须解决两个方面的基本问题:一是消除问题情境化设计中的认知偏差,即情境内容选取的偏差、思维方式预设的偏差和问题设计的偏差;
二是需要明确问题情境化设计的任务靶向,创设合适的情境化问题来承载任务靶向,更好地促进学生在知识理解、迁移与创生中,发展数学的核心素养.由此彰显问题情境化设计的教学意义,进而促进核心素养由课程理念向教学的现实转化.
[1] 中华人民共和国教育部.义务教育数学课程该标准(2022年版)[M].北京:北京师范大学出版社,2022:11.
[2] 夏小刚,张晶.基于学习体验的情境化问题设计[J].湖北教育(教育教学),2022(3):33-35.
[3] 王海青,曹广福.问题驱动数学教学的基本原则与思想及其实施步骤[J].数学教育学报,2022,31(1):24-27.
[4] 赵轩,任子朝,翟嘉祺.高考数学科情境化试题设计研究[J].数学通报,2021,60(12):1-3,66.
[5] 李健,李海东.情境在现实问题解决中的作用——基于5套人教版初中数学教科书的纵向比较[J].数学教育学报,2021,30(4):30-34,40.
[6] 任旭,夏小刚.问题情境的创设:基于思维发展的理解[J].数学教育学报,2017,26(4):15-18.
[7] 夏小刚.数学课堂热点问题讨论系列(4)本期话题:你创设的情境有意义吗?(续)情境创设≠情境的生活化、趣味化[J].人民教育,2006(9):24-26.
[8] 夏小刚,汪秉彝.数学情境的创设与数学问题的提出[J].数学教育学报,2003,12(1):29-32.
[9] 罗日叶.为了整合学业的获得:情景的设计和开发[M].2版.汪凌,译.上海:华东师范大学出版社,2010:41-42.
[10] 曹一鸣.数学教学中的“生活化”与“数学化”[J].中国教育学刊,2006(2):46-48,58.
[11] BIGGS J B,COLLIS K F.学习质量评价:SOLO分类理论:可观察的学习成果结构[M].高凌飚,张洪岩,译.北京:人民教育出版社,2010:3-4.
[12] 陈行,鲍建生,邢向东.国外数学任务设计研究50年:回顾与前瞻[J].课程·教材·教法,2018,38(7):139-143.
[13] 约翰·杜威.民主主义与教育[M].王承绪,译.北京:人民教育出版社,1990:179.
[14] 张夏雨.基于关系—表征复杂性模型的有背景问题难度研究[J].数学教育学报,2010,19(3):46-49.
[15] 邵志芳,刘永芳,钟毅平.关于问题难度的实验研究[J].心理科学,1996(5):278-281,320.
Cognitive Bias and Task Target in Situational Design of Mathematical Problems
ZHANG Jing1, 2, XIA Xiao-gang1
(1. School of Mathematics and Science, Guizhou Normal University, Guizhou Guiyang 550001, China;2. School of Science, Qiongtai Normal University, Hainan Haikou 571127, China)
In the era of literacy, two basic problems must be solved in mathematical problems situational design. First, the cognitive bias in the situational design should be eliminated, involving the bias in the situational content selection, the bias in the way of mathematical method preset and the deviation in the mathematical problem designing, so as to form a good match between the goal setting of the problem situation and students’ cognitive foundation of; Second, in order to enhance the effectiveness of problem-based contextualized teaching, it is necessary to clarify the task target of problem-based contextualized design, create appropriate contextualized problems to carry the task target, and better promote the development of students’ mathematical literacy in knowledge construction.
mathematical problems; situational design; cognitive bias; task target
G420
A
1004–9894(2022)06–0075–05
张晶,夏小刚.数学问题情境化设计中的认知偏差及任务靶向[J].数学教育学报,2022,31(6):75-79.
2022–07–05
全国教育科学“十三五”规划课题——面向核心素养的数学问题情境教学测评模型研究(XHA180286);
琼台师范学院校级一流本科课程建设项目(QTjg2022-52)
张晶(1984—),女,吉林集安人,琼台师范学院讲师,贵州师范大学博士生,主要从事数学教育研究.夏小刚为本文通讯作者.
[责任编校:周学智、张楠]
猜你喜欢靶向素养情境新型抗肿瘤药物:靶向药物中老年保健(2022年1期)2022-08-17如何判断靶向治疗耐药保健医苑(2022年5期)2022-06-10借助具体情境学习位置与方向数学小灵通·3-4年级(2021年3期)2021-04-13携IL-6单克隆抗体靶向微泡破坏技术在兔MI/RI损伤中的应用昆明医科大学学报(2021年2期)2021-03-29必修上素养测评 第四测新世纪智能(高一语文)(2020年10期)2021-01-04必修上素养测评 第三测新世纪智能(高一语文)(2020年10期)2021-01-04创设情境 以说促写作文成功之路·小学版(2020年6期)2020-07-27必修上素养测评 第八测新世纪智能(高一语文)(2020年12期)2020-06-01必修上素养测评 第七测新世纪智能(高一语文)(2020年12期)2020-06-01学理审思:真实情境写作之中考命题福建基础教育研究(2019年11期)2019-05-28