何声清
“等可能性偏见”对初中生古典概率内容学习进阶的影响
何声清
(上海师范大学 数理学院,上海 200234)
以713名七~九年级学生为被试,考查他们持有的“等可能性偏见”对古典概率学习进阶的消极影响及作用机制.结果表明:学生的“等可能性偏见”总体上随着年级递增呈消退态势,其中九年级是一个关键节点;
男、女生的“等可能性偏见”在程度上无显著性差异;
“等可能性偏见”与各概率任务的得分水平均呈显著性负相关;
“等可能性偏见”对学习进阶的作用机制是部分中介效果而非调节效果.对概率教学的启示有:遵循学生概率内容学习进阶的规律,精心设计数学任务和教学路径;
渗透“概率有相对大小”这一观念及发展构建样本空间的具体策略是消解“等可能性偏见”的两个关键举措.
等可能性偏见;
古典概率;
样本空间;
学习进阶;
中介效应;
调节效应
身处大数据时代,概率素养(probability literacy)已然成为公民数学素养培育的一项重要目标.在数学教育研究领域,国际学生测评项目(Program for International Student Assessment,简称PISA)将概率素养作为学生数学素养测评的内容维度[1],第12、13届国际数学教育大会(International Congress on Mathematics Education,简称ICME)也将其作为“概率学与教”专题研讨的焦点议题[2-3].
世界各国大都在中小学阶段的数学课程中设置了概率内容[4].中国《义务教育数学课程标准(2011年版)》在概率内容的编排方式上较其实验稿整体后移[5],《义务教育数学课程标准(2022年版)》则在该部分内容的设计上进一步凸显了从“定性认识”向“定量认识”的原则,其设计的知识发展主线是“感知随机性→了解简单随机现象中所有可能发生的结果→感知和定性描述可能性的大小→了解事件的概率”[6].上述发展主线与学生的学习进阶规律基本吻合:实证研究表明,学生的概率概念宏观上是在“感知随机性→定性比较概率的大小→构建样本空间(即枚举事件所有可能的结果)→概率的计算”等一系列步次中得以进阶的[7].
在初中阶段,课程预设的发展主线和学生实然的学习进阶都一致地聚焦于概率的定量刻画,即“(构建)样本空间→(据此)概率计算→(定量地)概率比较”.但事实上,上述学习进阶并非总是顺畅的.学生在接触学校课程的概率知识之前,已然积累了一定的直觉经验,它们不可避免地影响到其对于概率知识的学习[8].在大多数情况下,直觉经验对学生概率学习的影响是抑制性的,因此可称之为不良直觉.实证研究表明,关于概率的不良直觉在学前儿童[9]、小学生[10]、中学生[11]、大学生[12]甚至教师[13]群体中普遍存在.
“等可能性偏见”(equiprobability bias)是学生概率认知过程中出现的一种典型不良直觉.Lecoutre较早地对古典概率情境下的“等可能性偏见”做了界定:人们倾向于相信随机意味着均匀,随机事件在本质上是等概率的[14].例如,同时掷出两枚质地均匀的骰子,尽管“朝上点数之和为11”的概率是“朝上点数之和为12”的两倍,然而人们倾向于相信两者的概率相等.李俊将“等可能性偏见”划分为3个子类:假设一次试验共有个可能的结果,第一类迷信“这个可能的结果其概率均为1/2”,第二类认为“每一结果的可能性都为1/”,第三类认为“理论上相差不大的机会在一次试验中是相等的”[15].更一般地,人们在日常决策中也常暴露出其持有的“等可能性偏见”.例如,人们习惯性地用“50比50的机会”(fifty-fifty chance)这种“看似定量化的语言”描述“赛马获胜的概率”“投篮命中的概率”等诸多场景下的概率问题[16].究其原因,认为“只有两种可能的情况,它们非此即彼”(例如“要么获胜,要么失败”“要么命中,要么不中”)[12].事实上,这非但不是用“定量化的语言”描述概率,而恰恰是“拿不定主意”的内心写照[17].
在“样本空间→概率计算→概率比较”的学习进阶中,“等可能性偏见”便是其中的关键抑制性因素.例如新近一项研究表明,在古典概率问题情境中,学生首先须能够正确地构建样本空间,然后据此进行概率计算和比较.但如果他们持有“等可能性偏见”这一不良直觉,即便正确构建了样本空间也无法保证其能够规范地计算和比较概率[18].那么,“等可能性偏见”在学生古典概率内容学习进阶中的作用机制是什么?其影响效应如何?研究将厘清上述两个问题,据此为概率教学的改进提供实证依据.
2.1 被试
从山东省青岛市选取办学水平为优秀、良好及一般的3类学校,选取初中生被试合计713名.分类依据是:邀请该市教研员从升学率的角度将该地区学校划分成上述3个水平,并由该教研员从3个水平学校中分别选取一所,从每所学校分别选取七、八及九年级学生为被试.办学水平为优秀、良好及一般学校的被试分别为323名(占比45.3%)、244名(占比34.2%)及146名(占比20.5%),七、八及九年级被试分别为257名(占比36.0%)、229名(占比32.1%)及227名(占比31.8%),男性、女性被试分别为353名(占比49.5%)和357名(占比50.1%),另有3名被试性别信息缺失.更具体地,办学水平为优秀的学校中,七、八及九年级被试分别为114名、102名及107名,男性、女性被试分别为161名和162名;
办学水平为良好的学校中,七、八及九年级被试分别为94名、78名和72名,男性、女性被试分别为126名和118名;
办学水平为一般的学校中,七、八及九年级被试分别为49名、49名和48名,男性、女性被试分别为66名和77名(3名被试性别信息缺失).以上被试均采用人教版教材,该教材在九年级上册设置了“概率初步”一章,主要涉及“随机事件与概率”“用列举法求概率”及“用频率估计概率”的内容.
2.2 测查材料
2.2.1 古典概率测试
以“摸球”游戏为载体,测试包含5个问题(下文用Q表示).所有问题的情境均是:
不透明的盒子里有黑球、白球、绿球若干,各种颜色球大小、重量、质地、手感等均相同.摇晃盒子后,从中同时摸出两个球.
每个问题设计3个概率任务(下文用T表示),即样本空间(T1)、概率比较(T2)、概率计算(T3).以Q2为例.
(T1:样本空间)一共有几种可能的摸法?请列出它们.
(T2:概率比较)摸到“一黑一白”和“两个白球”的可能性哪个更大?抑或是一样大?
(T3:概率计算)摸出“一黑一白”的可能性有多大?
尽管从理论上说概率计算应早于概率比较,但结合课程标准设计的知识发展主线来看,在对概率进行定量性地计算之前,学生能够定性地进行概率比较,因此将概率计算放在了任务序列的最后.
对于同样的问题背景(即“不透明的盒子里有黑球、白球、绿球若干,各种颜色球大小、重量、质地、手感等均相同”),如果题意仅要求“从中摸出一个球”,学生在3个任务上的作答通常会出现“天花板效应”[19],因此研究不再涉及.鉴于未做标记的情况下难以辨别被试是否真正理解样本空间[20],研究在题目配图中对球做了序号标记.事实上,现行教材在设计“概率初步”内容时也进行了类似处理[21],因此这对学生而言并不陌生.

所有问题均采取选择题的方式,正确作答记1分,错误作答记0分.根据题目关涉的组合的复杂度,将问题区分为简单、中等、较难3个水平.需要说明的是:第一,这里关于题目复杂度的设计是基于理论分析得出的(如上所述);
第二,之所以按照当前的逻辑设计问题序列,目的是在确保问题结构、设问内容、设问方式完全一致的前提下,给被试呈现一个由易到难的问题序列,使其能有更好的作答体验.5个问题的设计思路详见表1.

表1 古典概率测试中5个问题的设计思路
2.2.2 “等可能性偏见”调查问卷
根据有关直觉测量研究的观点,直觉在人们决策中既有合理的方面又有朴素的方面,对于直觉的测量宜采用自我报告偏好的方法获取被试的“自然倾向”[23].鉴于此,研究采用5级Likert量表的形式测量学生概率推理中的直觉程度,由此获取的数据将比“是否持有某种直觉”的二元结论更加具体.“等可能性偏见”调查问卷共包含3个问题.根据问题的描述,要求被试结合自己的实际情况标定认可度.编码“1”至“5”按认可度递增依次表示“完全不同意”至“完全同意”.由于“等可能性偏见”是学生概率认知中的一个不良直觉,因此认可度越高表示该不良直觉的程度越深.确保一般性,问卷兼顾两种典型的等可能性偏见.例如:
(“1/2型”)篮球运动员库里的罚球命中率接近90%.在一次正常的罚球前,可以预测他命中的概率是1/2,因为球要么进,要么不进.
(“1/型”)班主任计划根据抽签的方式从4位同学中随机挑选两位打扫卫生,这4位同学中男生、女生各两名.俗话说“男女搭配,干活不累”.老师挑到“男女搭配”的概率为1/3,因为要么挑到“俩男生”,要么挑到“俩女生”,要么挑到“男女搭配”.
需要指出的是,在“1/2型”等可能性偏见的题项中,提及“罚球命中率为90%”这一信息是必要的,目的是给学生决策提供真实场景,考察学生在真实场景中的直觉水平.如果没有这一信息,考虑到“某位运动员的罚球命中率为50%”这一情况的存在,将使得学生在作答时产生过多的假设或纠结,反而造成测量数据不准确.因此,认为通过提供这一真实信息,能够更准确反映学生等可能性偏见这一直觉的真实情况,并且避免了题意可能带来的理解上的歧义.
2.2.3 验证性因子分析
以“样本空间”“概率比较”“概率计算”及“等可能性偏见”4个测查内容为并行一阶变量做多因素斜交模型的验证性因子分析.采用极大似然估计,得到“样本空间”的因子载荷分别为0.870、0.830、0.886、0.865及0.856,“概率比较”的因子载荷分别为0.779、0.819、0.823、0.820及0.814,“概率计算”的因子载荷分别为0.690、0.720、0.539、0.618及0.574,“等可能性偏见”的因子载荷分别为0.359、0.353及0.668,上述路径系数均大于0.35且达显著(所有<0.001),说明各显变量能有效反映其潜变量的特质.
模型的绝对配适度指标=0.059(小于0.08),增值配适度指标=0.939,=0.927,=0.955,=0.947,=0.955(均大于0.9),简约配适度指标=0.791,=0.805(均大于0.5),2/为3.469(小于5),以上指标均达配适标准,说明模型的配适度良好.
2.3 研究方法
采用调查法分别收集学生概率任务作答数据及“等可能性偏见”认可度数据;
采用描述性统计分析学生“等可能性偏见”的发展特征;
采用相关分析初步揭示“等可能性偏见”与概率任务作答表现的关系;
采用路径分析探索“等可能性偏见”在学习进阶中的中介效果和调节效果.
2.4 模型建构
根据课程标准的主线设计,古典概率的学习进阶是在“样本空间→概率计算→概率比较”这几个步次中向前推进的[7].另有实证研究表明,因受“等可能性偏见”的抑制效果,学生即便正确地构建了样本空间也无法保证其能够规范地计算和比较概率[18].研究中,“样本空间”任务主要涉及组合推理和枚举能力,学生在该任务上的表现理论上不受“等可能性偏见”的影响,而在“概率计算”和“概率比较”任务上的表现除了受其构建样本空间能力的积极影响外,还受到“等可能性偏见”这一不良直觉的消极影响.更微观地,如何刻画“等可能性偏见”对概率内容学习进阶的影响机制?综上分析,有两种基本假设是可以预见的.其一,样本空间概念的加深能够消解“等可能性偏见”,并且能够据此提升其概率计算和比较的能力;
类似地,概率计算能力的提升能够消解“等可能性偏见”,并且能够据此提升其概率比较的能力.其二,样本空间概念的加深能否提升概率计算和比较的能力取决于其“等可能性偏见”的程度;
类似地,概率计算能力的提升能否提升概率比较的能力取决于其“等可能性偏见”的程度.换言之,有无可能被试即便在T1中作答正确,但在T2及T3中非但没有基于T1的结果计算和比较概率,反而诉诸“等可能性偏见”认为“二者的概率相等,皆为1/2(或1/)”.
基于第一种假设,将“等可能性偏见”作为影响概率内容学习进阶的中介变量,构建如下模型.
模型1.在进阶序列“样本空间→概率比较”中,将“等可能性偏见”作为中介变量().“样本空间”对“概率比较”的直接作用(→)记为;
“样本空间”对“等可能性偏见”的直接作用(→)记为;
“等可能性偏见”对“概率比较”的直接作用(→)记为.
模型2.在进阶序列“样本空间→概率计算”中,将“等可能性偏见”作为中介变量().“样本空间”对“概率计算”的直接作用(→)记为;
“样本空间”对“等可能性偏见”的直接作用(→)记为;
“等可能性偏见”对“概率计算”的直接作用(→)记为.
模型3.在进阶序列“概率计算→概率比较”中,将“等可能性偏见”作为中介变量().“概率计算”对“概率比较”的直接作用(→)记为;
“概率计算”对“等可能性偏见”的直接作用(→)记为;
“等可能性偏见”对“概率比较”的直接作用(→)记为.
对于以上模型均有:
基于第二种假设,将“等可能性偏见”作为影响概率内容学习进阶的调节变量,构建如下模型.
模型4.在进阶序列“样本空间→概率比较”中,将“等可能性偏见”作为调节变量().“样本空间”对“概率比较”的直接作用(→)记为1;
“等可能性偏见”对“概率比较”的直接作用(→)记为2;
“样本空间”在“等可能性偏见”调节下对“概率比较”的作用(×→)记为3.
模型5.在进阶序列“样本空间→概率计算”中,将“等可能性偏见”作为调节变量().“样本空间”对“概率计算”的直接作用(→)记为1;
“等可能性偏见”对“概率计算”的直接作用(→)记为2;
“样本空间”在“等可能性偏见”调节下对“概率计算”的作用(×→)记为3.
模型6.在进阶序列“概率计算→概率比较”中,将“等可能性偏见”作为调节变量().“概率计算”对“概率比较”的直接作用(→)记为1;
“等可能性偏见”对“概率比较”的直接作用(→)记为2;
“概率计算”在“等可能性偏见”调节下对“概率比较”的作用(×→)记为3.
对于以上模型均有:
3.1 “等可能性偏见”的描述性统计
学生的“等可能性偏见”描述性统计结果显示,“等可能性偏见”的得分均值随年级递增逐步降低(七年级=3.32,=0.95;
八年级=3.28,=0.99;
九年级=2.96,=1.04).方差分析显示,各年级间得分均值差异在统计意义上达到显著((2, 710)=9.163,<0.001).LSD多重比较进一步显示,七、八年级之间差异不显著(七~八年级=0.04,=0.597),七年级与九年级、八年级与九年级之间则均达显著(七~九年级= 0.36,<0.001;
八~九年级=0.32,<0.01).以上表明:初中生持有的“等可能性偏见”总体上随着年级递增呈消退态势,其中九年级是一个关键节点.
独立样本检验显示,不同性别学生的“等可能性偏见”在程度上无显著性差异(男生=3.17,男生=1.04;
女生=3.22,女生=0.96;
=0.434).这也得到了国内其它地区被试实证研究的支撑[19].
3.2 关涉变量的相关分析
学生“等可能性偏见”的程度与其在样本空间、概率比较及概率计算任务上的得分水平均存在显著负相关性(1=-0.160,2=-0.259,3=-0.204;
所有<0.001),样本空间与概率比较、样本空间与概率计算、概率计算与概率比较之间在得分水平上均存在显著正相关性(4=0.483,5=0.539,6=0.747;
所有<0.001),以上均符合理论预期.性别与样本空间、概率比较及概率计算得分水平之间均存在显著相关性(7=0.090,<0.05;
8=0.102,<0.01;
9=0.122,<0.01),下面将其作为控制变量.上述变量的相关系数矩阵见表2.
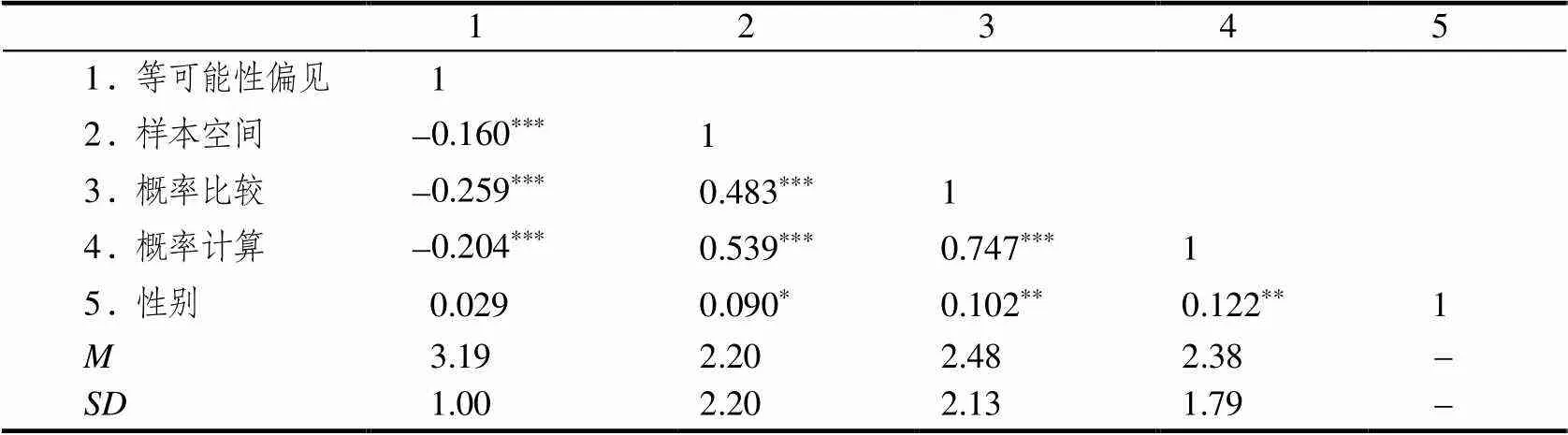
表2 关涉变量的相关系数矩阵
注:*表示<0.05,**表示<0.01,***表示<0.001
3.3 “等可能性偏见”在概率内容学习进阶中的作用机制
(1)进阶序列“样本空间→概率比较”的中介效果.
采用PROCESS插件进行中介效应的分析.重复随机抽取5 000个Bootstrap样本,采用偏差校正的Bootstrap方法检验中介效应(下同).
“样本空间”对“等可能性偏见”有负向影响且达显著(=-0.073;
=-0.106,=-0.039),对“概率比较”有正向影响且达显著(直接=0.432;
=0.370,= 0.494);
“等可能性偏见”对“概率比较”有负向影响且达显著(=-0.397;
=-0.533,=-0.261).
“样本空间”经由“等可能性偏见”对“概率比较”有正向间接影响且达显著(间接=0.029,=0.015,=0.048).模型的总体效应达到显著(总体=0.461,=0.398,=0.523),其中直接效应量占93.7%,间接影响效应量占6.3%;
模型能够解释因变量27.1%的变异(<0.001).以上表明,“等可能性偏见”在进阶序列“样本空间→概率比较”中存在部分中介效果.
模型1的非标准化系数及其显著性指标如表3所示.

表3 模型1的非标准化系数及其显著性指标
注:表示“样本空间”
(2)进阶序列“样本空间→概率计算”的中介效果.
“样本空间”对“等可能性偏见”有负向影响且达显著(=-0.073;
=-0.106,=-0.039),对“概率计算”有正向影响且达显著(直接=0.415;
=0.365,= 0.466);
“等可能性偏见”对“概率计算”有负向影响且达显著(=-0.217;
=-0.328,=-0.105).
“样本空间”经由“等可能性偏见”对“概率计算”有正向间接影响且达显著(间接=0.016,=0.007,=0.030).模型的总体效应达到显著(总体=0.431,=0.380,=0.481),其中直接效应量占96.3%,间接影响效应量占3.7%;
模型能够解释因变量30.9%的变异(<0.001).以上表明,“等可能性偏见”在进阶序列“样本空间→概率计算”中存在部分中介效果.这也得到了访谈资料的支撑.
访谈一位七年级的被试,该被试在所有Q2T1中的作答错误,在Q2T3中选择“1/3”.
师:第二题的第一问,你说一种有三种可能的情况,为什么?
生:嗯.一黑一白、两白、两黑.
师:好的.第三问你认为可能性是1/3.理由是什么?
生:因为有三种情况,它们的机会是均等的.
师:(它们的概率)真的彼此相等吗?
生:要不然呢?
师:我们来做个试验吧(限于篇幅,过程略).
……
师:现在我告诉你另一种办法(在稿纸画出Q2的插图).
师:你看这个图,有两个黑球和两个白球.你想象一下,闭上眼睛同时摸出两个球.是不是有可能摸到的都是白球(画示意图),还有可能摸到的这个黑球和这个白球(画示意图),……总的来说,摸到“1个黑球和1个白球”有4种可能的搭配,摸到“2个白球”只有这一种搭配?
生:是的.它的搭配多,所以可能性就更大.
师:关键的问题在于:你最初认为摸出的球一共只有3种可能的情况.
师:当你知道了一共有6种可能的搭配后,有没有真正认识到:两者的概率可以从理论上、从数学上来推理?
生:是的.
师:你还坚持认为“两者的可能性一样大”吗?
生:应该一个是4/6,一个是1/6.
从上述访谈可以发现,该被试缺乏对样本空间的认识,在概率决策时表现出“等可能性偏见”(第二类).研究者引导被试审视最初的想法,帮助其采用连线法构建样本空间,使其认识到依据样本空间可以计算和比较概率.该被试意识到自己之前的错误理解,并纠正了在其它问题上的错误作答.这说明,当学生掌握了组合知识、加深了对样本空间的认识,是有可能放弃原先持有的“等可能性偏见”的,从而能够正确地计算和比较概率.
模型2的非标准化系数及其显著性指标如表4所示.

表4 模型2的非标准化系数及其显著性指标
注:表示“样本空间”
(3)进阶序列“概率计算→概率比较”的中介效果.
“概率计算”对“等可能性偏见”有负向影响且达显著(=-0.115;
=-0.156,=-0.074),对“概率比较”有正向影响且达显著(直接=0.858;
=0.799,= 0.918);
“等可能性偏见”对“概率比较”有负向影响且达显著(=-0.237;
=-0.343,=-0.132).
“概率计算”经由“等可能性偏见”对“概率比较”有正向间接影响且达显著(间接=0.027,=0.014,=0.046).模型的总体效应达到显著(总体=0.886,=0.827,=0.944),其中直接效应量占96.9%,间接影响效应量占3.1%;
模型能够解释因变量56.8%的变异(<0.001).以上表明,“等可能性偏见”在进阶序列“概率计算→概率比较”中存在部分中介效果.
模型3的非标准化系数及其显著性指标如表5所示.

表5 模型3的非标准化系数及其显著性指标
注:表示“概率计算”
(4)在上述进阶序列中的调节效果.
上述结果证实了第一种研究假设,即“等可能性偏见”在概率内容学习进阶中起到中介效果.它在影响学习进阶时是否还有其他作用机制呢?接下来对第二种研究假设进行验证,即“等可能性偏见”在概率内容学习进阶中是否起到调节效果.
在模型4中,“样本空间”对“概率比较”有正向影响且达显著,路径系数及其显著性指标同模型1,“等可能性偏见”对“概率比较”有负向影响且达显著(2=-0.402;
=-0.539,=-0.265);
在模型5中,“样本空间”对“概率计算”有正向影响且达显著,路径系数及其显著性指标同模型2,“等可能性偏见”对“概率计算”有负向影响且达显著(2=-0.214;
=-0.326,=-0.102);
在模型6中,“概率计算”对“概率比较”有正向影响且达显著,路径系数及其显著性指标同模型3,“等可能性偏见”对“概率比较”有负向影响且达显著(2=-0.241;
=-0.347,=-0.135).
但是,以上模型的交互项路径系数均未达显著(模型4:=0.684=-0.040,=0.082;
模型5:=-0.415,=-0.060,=0.039;
模型6:=0.979,=-0.030,=0.089).以上说明,“等可能性偏见”在上述进阶序列中的调节效果不存在,即证伪了第二类研究假设.
模型4、5、6的非标准化系数及其显著性指标如表6所示.

表6 模型4—6的非标准化系数及其显著性指标
4.1 初中生持有的“等可能性偏见”虽呈消退态势但总体上比较顽固
研究表明,初中生持有的“等可能性偏见”具有如下发展特征:七、八年级在程度上大体相当,九年级则有所消退,但总体上比较顽固.其原因体现在以下方面.
第一,源于朴素经验的影响,使得不良直觉不可避免地长期交织在学生概率认知的过程中.日常生活中充斥着大量的随机现象,市井信息中蕴含着纷繁的概率问题.在接触学校课程里的概率知识之前,人们已然基于生活的经验孕育了它的模糊概念,这其中就广泛存在着朴素的、不良的直觉,它们常常消极地影响着对于概率的正确认知[8].例如,人们常常将“随机”引申为“随意”(即“随我的心意”),认为随机事件的概率可以被控制[24];
甚至做出“我愿意让机会平等,相信各个结果的概率是均等的”等判断[19].诸多研究一再证实,概率认知中的不良直觉甚至在大学生[12]及教师[13]群体都广泛存在且十分顽固.与其它不良直觉的发展特征类似,由于朴素经验的影响,人们持有的“等可能性偏见”通常也比较顽固、难以消退.这不仅得到国外实证研究的支撑[14,25-28],还得到了基于国内其它地区被试实证研究的支撑[19].至于学生的“等可能性偏见”能否在高中阶段有进一步的消退甚至消除,尚待做进一步实证研究.
第二,源于样本空间概念的发展,使得九年级学生持有的“等可能性偏见”在掌握概率计算的规范策略后有所消退.人教版教材在九年级上册第二十五章“概率初步”第一节“随机事件与概率”中结合具体案例明确提及“随机事件发生的可能性是有相对大小的”[21],这使得学生初步动摇其持有的“等可能性偏见”,即“不能一味地迷信所有事件的概率都相等”.紧接着,在第二节“用列举法求概率”中具体学习了通过列表法和树状图法构建样本空间的策略,并详细结合“同时抛两枚硬币”“同时掷两枚骰子”等实例展示了上述策略的具体应用[21],进一步完善了其概率计算和比较的策略,即借助上述两种方法枚举试验可能出现的所有结果以及目标事件所含的所有结果,最后根据古典概率的计算公式求解.研究也证实,学生样本空间概念的加深能够消解其持有的“等可能性偏见”,并且能够据此提升其概率计算的能力;
学生概率计算能力的提升能够消解其持有的“等可能性偏见”,并且能够据此提升其概率比较的能力.综上分析,样本空间概念的发展是使得九年级学生“等可能性偏见”有所消退的原因.
4.2 “等可能性偏见”对概率内容学习进阶的作用机制是中介效果而非调节效果
“等可能性偏见”对于学生概率学习的消极影响毋庸赘言.一项新近研究指出,学生需要先理解样本空间,即能够列举试验所有可能的结果,才能够据此量化某事件的概率并将其与其它事件的概率作比较.在这个过程中,有些学生即便能够正确构建样本空间,但与此同时也持有“等可能性偏见”,因此这一不良直觉的程度也是甄别其是否真正理解了概率概念的重要证据[18].
但是,上述研究没有更具体地指出“等可能性偏见”究竟是如何抑制学生概率学习的.换言之,基于上述研究结果可以就“等可能性偏见”作用于概率学习进阶的微观机制提出两种基本假设.其一是中介效果,即理解了样本空间,就具备了量化概率的潜力,但同时因持有“等可能性偏见”会抑制该潜力;
具备了量化概率的能力,就具备了比较概率的潜力,但同时因持有“等可能性偏见”会抑制该潜力;
尽管“等可能性偏见”的抑制作用存在,但样本空间概念的加深、概率计算策略的发展都能够使其得以有所消退.其二是调节效果,即样本空间概念的加深能否提升概率计算的能力取决于其“等可能性偏见”的程度;
概率计算能力的提升能否提升概率比较的能力取决于其“等可能性偏见”的程度.
研究证实,“等可能性偏见”对概率内容学习进阶的作用机制是中介效果而非调节效果,这对于概率教学有两点基本启示.其一,但凡持有“等可能性偏见”,学生概率内容的学习进阶都会受到抑制,教学应有意识地帮助其消除这一不良直觉.其二,按照学生学习进阶的客观规律进行教学十分重要且必要,即遵循“样本空间→概率计算→概率比较”的进阶步次,精心设计数学任务和教学路径.在这其中,渗透“概率有相对大小”这一观念及发展构建样本空间的具体策略是消解“等可能性偏见”的两个关键举措,这事实上也解释了该不良直觉在九年级时得以有所消退原因.更一般地,对于整个数学学科来说,学生一旦对处于下位的法则、程序及观念的理解是碎片化的,那么他们在解决上位问题时诉诸不良策略或直觉的倾向性就明显增加[18].
(1)初中阶段学生持有的“等可能性偏见”总体上随着年级递增呈消退态势,其中九年级是一个关键节点;
男、女生持有的“等可能性偏见”在程度上无显著性差异.
(2)学生持有的“等可能性偏见”与其在各概率任务上的表现均呈显著性负相关,对概率内容学习进阶有显著的抑制作用.
(3)学生持有的“等可能性偏见”在其学习进阶中起到部分中介效果,即证实了第一种研究假设.
(4)学生持有的“等可能性偏见”在其学习进阶中的调节效果不存在,即证伪了第二种研究假设.
研究存在两点不足.第一,通过邀请教研员根据升学率指标从3类学校中分别选取一所学校作为样本,存在代表性不足的问题.第二,考虑到学生在九年级学习了“用列举法求概率”等知识,若以该年级学生为被试探索3个变量的作用机制,或许会有更丰富的结果.未来研究将进一步扩大样本量,并针对不同年级被试分别进行作用机制的分析.
[1] LANGE J. Mathematical literacy for living from OECD-PISA perspective [J]. Tsukuba Journal of Educational Study in Mathematics, 2006 (25): 13-35.
[2] NILSSON P, LI J. Teaching and learning of probability [M] // CHO S J. The proceedings of the 12th international congress on mathematical education: Intellectual and attitudinal challenges. New York: Springer, 2015: 437-442.
[3] BATANERO C, CHERNOFF E J, ENGEL J, et al. Topic study group No. 14: Teaching learning of probability [M] // KAISER G. The proceedings of the 13th international congress on mathematical education. Cham: Springer, 2017: 439-442.
[4] 曹一鸣.十三国数学课程标准评价(小学初中卷)[M].北京:北京师范大学出版社,2012:9-11.
[5] 中华人民共和国教育部.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012:25-40.
[6] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022:74-76.
[7] 何声清,巩子坤.6~14岁儿童概率概念学习进阶[J].课程·教材·教法,2017,37(11):61-67.
[8] SHARMA S. Cultural influences in probabilistic thinking [J]. Journal of Mathematics Research, 2012, 4 (5): 63-77.
[9] KAFOUSSI S. Can kindergarten children be successfully involved in probabilistic tasks [J]. Statistics Education Research Journal, 2004, 3 (1): 29-39.
[10] PRATT N C. Is chance fair? One student’s thoughts on probability [J]. Teaching Children Mathematics, 2005, 12 (2): 83-89.
[11] ZIMMERMANN G M, JONES G A. Probability simulation: What meaning does it have for high school students [J]. Canadian Journal of Science, Mathematics and Technology Education, 2002, 2 (2): 221-236.
[12] ALBERT J. College students’ conceptions of probability [J]. The American Statistician, 2003 (57): 37-45.
[13] LIU Y, THOMPSON P. Teachers’ understanding of probability [J]. Cognition and Instruction, 2007, 25 (2): 113-160.
[14] LECOUTRE M P. Cognitive models and problem spaces in “purely random” situations [J]. Educational Studies in Mathematics, 1992 (23): 557-568.
[15] 李俊.中小学概率的教与学[M].上海:华东师范大学出版社,2003:58.
[16] BRUINE B W, FISCHHOFF B, MILLSTEIN S G, et al. Verbal and numerical expressions of probability: ‘‘It’s a fifty–fifty chance” [J]. Organizational Behavior and Human Decision Processes, 2000, 81 (1): 115–131.
[17] FISCHHOFF B, BRUINE B W. Fifty-fifty = 50% [J]. Journal of Behavioral Decision Making, 1999 (12): 149-163.
[18] MORSANYI K, SZUCS D. Intuition in mathematical and probabilistic reasoning [M] // COHEN K R, DOWKER A. The Oxford handbook of numerical cognition. Oxford, UK: Oxford University Press, 2014: 137-153.
[19] 何声清,巩子坤.七~九年级学生概率认知中的“等可能性偏见”研究[J].数学通报,2017,56(6):13-17.
[20] 何声清,巩子坤.七~九年级学生概率比较的策略及其发展[J].数学教育学报,2017,26(2):41-45.
[21] 林群.义务教育数学教科书(九年级上册)[M].北京:人民教育出版社,2013:129,132,136-140.
[22] 何声清.“代表性启发”对初中生古典概率内容学习进阶的影响[J].数学教育学报,2020,29(4):27-33.
[23] PRETZ J E, BROOKINGS J B, CARLSON L A, et al. Development and validation of a new measure of intuition: The types of intuition scale [J]. Journal of Behavioral Decision Making, 2014, 27 (5): 454-467.
[24] GREER B. Understanding probabilistic thinking: The legacy of E. Fischbein [J]. Educational Studies in Mathematics, 2001 (45): 15-33.
[25] CHIESI F, PRIMI C. Recency effects in primary-age children and college students [J]. International Electronic Journal of Mathematics Education, 2009, 4 (3): 259-274.
[26] GURBUZ R, BIRGIN O. The effects of computer-assisted teaching on remedying misconception: The case of the subject “probability” [J]. Computers & Education, 2011 (58): 931-941.
[27] FALK R LANN A. The allure of equality: Uniformity in probabilistic and statistical judgment [J]. Cognitive Psychology, 2008 (57): 293-334.
[28] MORSANYI K, HANDLEY S J, SERPELL S. Making heads or tails of probability: An experiment with random generators [J]. British Journal of Educational Psychology, 2013 (3): 379-395.
The Impact of Equiprobability Bias on Junior School Students’ Learning Progressions of Classic Probability
HE Sheng-qing
(Mathematics and Science College, Shanghai Normal University, Shanghai 200234, China)
The present study selected 713 students in the seventh to ninth graders as the subjects and analyzed the negative impact and its mechanism of equiprobability bias on learning progressions of classic probability. The results shown that: first, students’ equiprobability bias generally decreases with the increase of grades, and the ninth grade is a key point; Second, there is no significant difference in the degree of equiprobability bias between boys and girls; Third, there is a significant negative correlation between equiprobability bias and the performance of each probability task; Fourth, the mechanism of equiprobability bias on learning progressions of classic probability is a partial mediating effect rather than a moderating effect. The enlightenment to probability teaching is as follows: on the one hand, conforming to the rule of students’ learning progressions of classic probability and designing elaborated mathematics tasks and teaching trajectories; On the other hand, penetrating the concept that probability is calculable and developing specific strategies to construct sample space are two key measures to eliminate equiprobability bias.
equiprobability bias; classic probability; sample space; learning progressions; mediating effect; moderating effect
G632.0
A
1004–9894(2022)06–0052–08
何声清.“等可能性偏见”对初中生古典概率内容学习进阶的影响[J].数学教育学报,2022,31(6):52-59.
2022–08–07
上海市浦江人才计划项目——初中生数学核心概念学习进阶及其影响因素的模型构建研究(2019PJC079)
何声清(1988—),男,安徽安庆人,讲师,博士,主要从事数学教育研究.
[责任编校:张楠、陈汉君]
猜你喜欢进阶直觉显著性一种结合多尺度特征融合与像素损失加权的显著性目标检测方法黑龙江大学自然科学学报(2022年1期)2022-03-29拉马努金——天才的直觉新世纪智能(数学备考)(2021年5期)2021-07-28直觉为舵 意象为帆——儿童直觉线描的“意象”表现教学实践少儿美术(2021年6期)2021-04-26林文月 “人生是一场直觉”海峡姐妹(2020年7期)2020-08-13一个“数学直觉”结论的思考新世纪智能(数学备考)(2020年12期)2020-03-29点电荷的平衡与非平衡问题的进阶学习中学生数理化(高中版.高二数学)(2020年1期)2020-02-20基于区域特征聚类的RGBD显著性物体检测小型微型计算机系统(2019年4期)2019-05-05传祺GM6:家用MPV新进阶汽车观察(2019年2期)2019-03-15基于显著性权重融合的图像拼接算法电子制作(2019年24期)2019-02-23欧盟法院判决明确欧盟商标通过使用获得显著性的地域认定标准中国知识产权(2018年12期)2018-12-29