郭书生,陈现军,廖高龙,王世越,赵 凯
(1.中海石油(中国)有限公司海南分公司,海南海口 570312;
2.中法渤海地质服务有限公司湛江分公司,广东湛江 524057;
3.西安石油大学石油工程学院,陕西西安 710065)
地层压力即地层孔隙流体的压力,正常情况下等于静水压力。超压是指地层压力大于静水压力的现象,也称为异常高压[1]。异常高压成因复杂,Magara[2]和Chapman[3]将其归为自源超压、邻源超压和他源超压3大类;
Ward等[4]提出了基于沉积压实过程力学关系的异常高压分类方法;樊洪海等[5-7]在其理论基础上,将异常高压的可能形成机制分为欠压实、构造运动、流体膨胀(卸载)和浮力作用4大类。莺歌海盆地乐东区深部地层存在大量的异常高压现象,前期认为主要属于单一的欠压实或流体膨胀成因,但随着现场钻井作业增多,研究发现通过基于单成因理论的Eaton法或Bowers法计算的地层压力与实际存在较大偏差,实际存在明显的卸载现象以及复合成因超压的特征。目前针对单成因超压地层超压机制判别方法主要包括测井曲线组合法、Bowers有效应力法和Bowers声波-密度交会图法等[8-18],而对于复合成因超压地层超压机制判识方法尚未达成共识。超压定量评价方法主要包括Eaton法和Bowers法,均已在现场广泛应用。Eaton法仅适用于加载型超压计算,Bowers法中的卸载方程仅适用于卸载型超压计算,二者并不适用于复合成因超压计算。张凤奇等[19]提出了一种计算流体膨胀、超压传递和构造应力诱发超压定量贡献的计算方法,该方法假设地层压力升高后声波速度不变,实际上由于岩石骨架的卸载以及油气的生成等作用将导致声波速度改变,因此该假设下超压值低于实际值。刘桃等[20]基于岩石应力-应变机制及岩石孔隙结构,建立了欠压实与流体膨胀成因的评价模型,进行了现场应用。该方法通过超压段密度的异常计算欠压实产生的加载型超压,认为剩余超压即为卸载型超压,但深部岩石属于非理想塑性体,流体膨胀引起岩石体积的扩容也会导致密度异常。目前缺乏有效的复合成因超压地层的孔隙压力计算方法。笔者从模拟加载、卸载超压岩石的力学响应特征出发,构建岩石应力-应变关系与岩石应力-密度关系的转化方法,拟合岩石的加载、卸载过程中有效应力-密度特征曲线,利用所建立的特征曲线,结合所建立的单成因贡献率计算模型,实现复合成因超压中单成因贡献率的定量评价。
莺歌海盆地乐东区中深部地层的地质分层由上到下依次为Y1段、Y2段、H1段和H2段,存在不同程度的超压现象。利用传统复合成因超压识别方法分别判识时,存在解释结果自相矛盾的现象。结合乐东区测井资料的特征,首先利用多井测井曲线组合法判识超压成因复杂度,再利用Bowers声波速度-密度交会图确定地层的超压成因。多井测井曲线组合法主要采用的是对超压更为敏感的声波时差测井资料来进行超压成因识别,并且认为声波时差一致性的较大幅度偏离正常压实趋势线时代表单一不均衡压实(欠压实超压);
Bowers法认为不均衡压实引起的超压位于加载曲线上,而流体膨胀造成的超压则位于卸载曲线上。利用多井测井曲线组合法,对该区域11口井定性判别其超压成因复杂度,如图1所示。图1中Y1段声波时差未偏离正常趋势线,为正常压力地层;
Y2段数据出现明显偏离但数据点较为集中,H1段数据点同样偏离趋势线但较为离散,H2段数据点最为离散。据此可以判断Y2、H1和H2段地层均存在超压,且超压成因复杂程度依次递增。

图1 多井测井曲线组合法确定超压成因复杂度图版Fig.1 Complexity chart of overpressure cause analyzed by multiwell logging curve
基于超压成因复杂程度的定性认识,采用Bowers声波速度-密度交会图法对Y2段、H1段和H2段地层超压成因类型进行分析,如图2所示。图2中绿线为Bowers加载特征曲线,加载型超压的特征表现为数据点落在加载特征曲线上,超压段测井声波速度和密度均减小;
蓝线为Bowers卸载特征曲线,卸载型超压的特征表现为数据点落在卸载特征曲线上,超压段测井声波速度减小,但密度基本保持不变;
分布在加载特征曲线和卸载特征曲线之间的点可被归结为复合成因超压,若其分布更为靠近卸载曲线,则复合成因中卸载的贡献比例较大,反之,加载的贡献比例较大。图2中数据点分布趋势表明Y2段部分井为加载型超压,部分井为卸载型超压;
H1、H2段属于复合成因超压,但由于H2段数据点更为靠近卸载曲线,因此该段卸载的贡献比例较大。最终确定莺歌海盆地乐东区中深部地层的超压成因为:Y2段属于加载、卸载型超压;H1、H2段属于复合型超压,且H2段中卸载的贡献比例较大。

图2 Bowers声波-密度交会图法确定超压成因图版Fig.2 Overpressure cause analyzed by Bowers s sonic-density crossplot method
莺歌海盆地乐东区H1、H2段属于复合超压,为了定量评价其单成因贡献,首先需要确定加载和卸载特征曲线。加载曲线可通过将建立的正常压实地层密度沿井深进行积分,并减去正常孔隙压力,即可获得正常压实地层的密度-有效应力特征曲线,根据等效深度原理,此曲线也是加载型超压的特征曲线。有效应力计算式为
(1)
式中,σeff为有效应力,MPa;
ρ为地层体积密度,g/cm3;p为正常孔隙压力,MPa;
g为重力加速度,取9.81 m/s2。
有效应力和密度的关系可通过泰勒公式展开,但在实际求解过程中发现存在一定误差,因此通过三次样条插值方法对σeff和ρ插值,得到莺歌海盆地的加载特征曲线如图3所示。
卸载曲线传统上采用Bowers卸载方程,但是其认为深部岩石已进入塑性状态,流体膨胀增压造成岩石骨架应力卸载,基本无变形恢复,密度基本不变。实际上地层岩石骨架应力卸载时变形存在部分恢复,密度也会发生变化。本文中利用室内岩石的三轴卸载过程精确评价卸载方程。
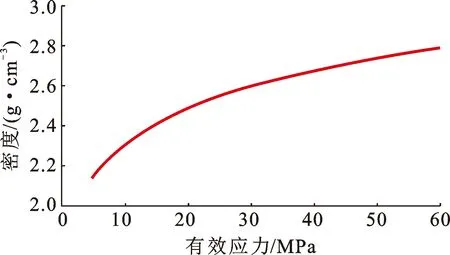
图3 莺歌海盆地加载特征曲线Fig.3 Loading characteristic curve of Yinggehai Basin
室内岩石的三轴卸载过程中体积应变的表达式为
(2)
式中,εv为体积应变;
V0和V分别为岩石初始体积和在一定有效应力下的体积,m3;
ρ0和ρ分别为岩石初始密度和在一定有效应力下的密度,kg/m3;
m为岩石质量,为定值,kg。
通过对式(2)变形可得一定有效应力下岩石的密度为
(3)
对莺歌海盆地8块岩心进行三轴压缩试验并分别计算其卸载过程中密度随有效应力的变化,如图4所示。对数据进行回归可以看出,在不同有效应力下的卸载曲线彼此平行,密度随有效应力的变化可被简化为线性关系。在实际应用中只需测量计算岩心卸载过程中单位有效应力降低对应的密度减小值即可绘制不同深度处的卸载曲线:
(4)
式中,σ为当前深度对应的有效应力,MPa;
ρ为卸载线上有效应力为σ时对应的密度,g/cm3;
σH和ρH分别为卸载点处的有效应力和密度。
对于任意深度均可得到其加载和卸载特征曲线,为后续的单成因贡献率定量评价提供评价方程。

图4 三轴压缩试验计算密度随有效应力变化Fig.4 Change of calculated density with effective stress in triaxial compression test
地层超压原因复杂多样,既包括欠压实、构造运动等相对前期的岩石骨架变形相关因素,也包括水热膨胀、生烃增压等相对后期的孔隙内流体作用相关因素,但从力学上均可归为加载型和卸载型两类。因此对于复合超压地层,可通过建立的加载和卸载特征曲线结合相关的数学模型,实现定量评价其单成因贡献率。地层单成因超压与复合成因超压的关系如图5所示。
复合成因超压总地层压力当量密度的表达式为
pp=p1+p2+p0.
(5)
式中,pp为地层压力当量密度,g/cm3;
p1和p2分别为加载型和卸载型超压当量密度,g/cm3;
p0为正常静水压力当量密度,通常取1.03 g/cm3。
仅考虑单成因时加载、卸载超压对应的岩石密度分别为
(6)
式中,ρ1和ρ2分别为仅考虑加载型超压、卸载型超压时岩石的密度,g/cm3;
f1和f2分别为加载特征方程和卸载特征方程;
σv为上覆岩层压力当量密度,g/cm3。

图5 地层单成因超压与复合成因超压关系Fig.5 Relationship between single genetic overpressure and polygenetic overpressure
方程组中p1、p2、ρ1、ρ2均为未知量,若要方程组封闭,还需要2个方程。构建复合成因超压地层岩石密度与单成因超压地层密度之间的关系,考虑到孔隙压力可由加载型、卸载型和静水压力线性叠加构成,对复合成因超压地层的密度进行叠加,即
ρ=c1ρ1+c2ρ2+c0ρ0.
(7)
式中,c1、c2和c3为系数,且c1+c2+c3=1。
由于密度主要受有效应力的影响,而一定深度时有效应力与地层压力和为定值,因此密度与当前地层压力有关。取c1=p1/pp、c2=p2/pp、c0=p0/pp,式(7)可写为
(8)
联立式(5)~(8)可迭代求解p1、p2,c1、c2即为单成因贡献率。迭代算法流程如图6所示。

图6 迭代求解单成因贡献率流程Fig.6 Iterative solution flow chart of single cause contribution rate
乐东A井的构造紧邻下伏梅山组、三亚组主力烃源岩层,成熟的烃类流体依靠源岩内超压驱动,以底辟活动波及区的垂向微裂隙为输导系统,由下部高势区向上部低势区运移,同时在构造脊背景的控制下,向优势运移方向聚集,最后在水道砂或海底扇储层圈闭中富集成藏,并且认为黄流组一段的超压为多成因,该井在3 911 m实测孔隙压力、上覆岩层压力、区域静水压力当量密度分别为2.20、2.29和1.03 g/cm3。
通过求解建立的方程组可得到单成因的贡献率,计算结果如表1所示。卸载型成因的贡献率为40.9%,因此该井黄流组一段主要的超压成因为卸载型成因。

表1 乐东A井单成因的贡献率
从岩石力学试验出发,建立了岩石密度-有效应力的关系图版。该图版克服了Bowers法对岩石理想塑性假设的不足,认为岩石的密度随有效应力发生改变,从而为复合成因超压中单成因贡献率的定量评价提供了基础。基于新的加载、卸载曲线,建立了岩石复合成因超压孔隙压力叠加模型和单成因超压贡献率求解模型。通过岩石密度和有效应力的关系,引入辅助方程,完成了对加载型超压、卸载型超压贡献的求解,进一步明确了超压机制。乐东区A井黄流一段加载型超压贡献率为12.3%,卸载型超压贡献率为40.9%,超压成因以卸载型为主,与现有的认识相符,该模型可以有效的定量评价复合成因超压中单成因超压的贡献率。
猜你喜欢声波测井贡献率本期广告索引测井技术(2022年3期)2022-11-25一种通用的装备体系贡献率评估框架军事运筹与系统工程(2020年2期)2020-11-16爱的声波 将爱留在她身边中国宝玉石(2018年3期)2018-07-09关于装备体系贡献率研究的几点思考军事运筹与系统工程(2018年3期)2018-03-26声波杀手小猕猴智力画刊(2017年6期)2017-07-03声波实验小溪流(画刊)(2017年5期)2017-06-15基于测井响应评价煤岩结构特征中国煤层气(2015年4期)2015-08-22中石油首个全国测井行业标准发布中国质量与标准导报(2015年2期)2015-02-28核磁共振测井在致密油储层孔隙结构评价中的应用天然气勘探与开发(2014年2期)2014-02-28声波大炮智慧与创想(2013年5期)2013-06-25