王 涛,倪学波,余国银,刘强明
(1.滁州学院 应急管理学院,安徽 滁州 239000;
2.滁州市消防救援支队,安徽 滁州 239000)
在制订城市交通应急预案时,为了有效提高应急救援处置能力,实现救援与疏散的快速展开,需要构建面向事故应急处置和救援演练的交通数据可视化与交通仿真辅助决策平台,以便对应急情况下交通预案的合理性、可行性、协调性以及其功效进行评估[1]。
例如,近几年Naboureh等[2]在城市应急交通(road emergency stations,RESs)的仿真最优化研究中,对包括尾气污染、安全、环境、可共用区、非可共用区、道路类型、事故易发区域、道路服务水平、性能半径在内的9项内容进行了仿真建模评价,其成果可用于城市突发事件带来的应急交通流管理中的决策支持。李俊捷等[3]在对跨区域综合交通运输网应急救援预案的研究中,将指标体系分为预案体系结构、应急工作流程及日常管理3个方面,为交通应急预案仿真模型的使用场景建立了初步的框架。汪欣国等[4]的道路运输安全评价模型,就是建立在一种仿真模型的基础上,为城市安全水平的变化提供参考依据。
人、车、路是道路交通的3项基本构成要素,城市应急交通仿真是对这3项要素在发生突发事件时所形成的交通流的动态模拟,通常应该包括交通流仿真建模、模型校准和仿真度验证等几个方面。
在交通流仿真建模理论方面,“自由流-同步流-堵塞流”三相理论是研究热点,Kerner等提出三相交通理论[5]后, 提出了一种微观仿真模型[6],该模型的计算机仿真基础是元胞自动机[7],Kerner-Klenov-Wolf (KKW)模型在模拟交通瓶颈诱发的交通拥塞模式图谱方面,得到了比基本图方法更符合实际观测的模拟结果,也因此得到了世界各国学者的认同。
为了使KKW模型更加符合交通实际,文献[8-12]对KKW模型进行了有效的改进,但是在应急交通仿真方面仍然有以下问题未得到解决。
1)在KKW模型及其改进模型中,仅提出了一种同步函数来模拟车辆状态,未考虑突发事件时由于交通管制,道路通行规则突然改变,驾驶员驾驶决策的变化问题,以及其他随机因素的扰动问题。
2)在KKW模型及其改进模型(也包括车辆跟驰模型)中,主要考虑的是前车对后车的影响(包括车头距、相对速度等),但是应急状态下,后车对前车的影响并未涉及,例如,应急状态时,后车鸣笛等因素对前车各种影响在这一类模型中未进行深入分析。
3)在三相交通流模型中,一般只是提出仿真模型,并只进行数值分析,未将仿真模型的数据和真实的交通流数据进行对比分析,未证实其仿真的准确度。
本文对DDM模型[13]进行了完善,使其可以满足道路交通的应急状态管理,在基本图仿真分析的基础上,对如何进行主要参数的校准进行了说明,并对本模型进行了时间序列分析和真实交通数据拟合。
1.1 模型提出
所提出的DDM由驾驶决策函数驱动,见公式(1):
Hn(t+1)=Fchange{Hn(t),Pc}
(1)
各种驾驶模式的切换模态如式(2)所示:
(2)
驾驶模式Hn的切换方式如表达式(3)所示。
(3)
由公式(3)可知,当在进行驾驶时,车辆所形成的交通流的状态会发生以下模式的改变:
1)Mode0→Mode1,此时后车的速度大于前车,且车头距不足,自动进入Mode1(同步流)模式。
2) 此时后的速度大于前车,且车头距不足,自动进入Mode2(堵塞流)模式。
3)Mode2→Mode1,相邻两车的车头距较长时,可进入 Mode1(同步流)模式。
4)Mode1→Mode0,相邻两车车头距较长,且不影响后车加速时,进入Mode0(自由流)模式。
为了保证驾驶员的行驶模式的随机性,在模型中设置了Pc作为“换档”概率。
1.2 基本图分析
在一般的基本图理论中将交通量之间的函数关系描述为固定函数关系曲线,但是这与实际的交通观察不符,并被国内外的学者所证实,在三相同步流理论中,交通量之间的关系会被认为是不具有固定函数的二维区间,如图1所示,其中a为三相交通流示意图,b为实测拟合数据图。
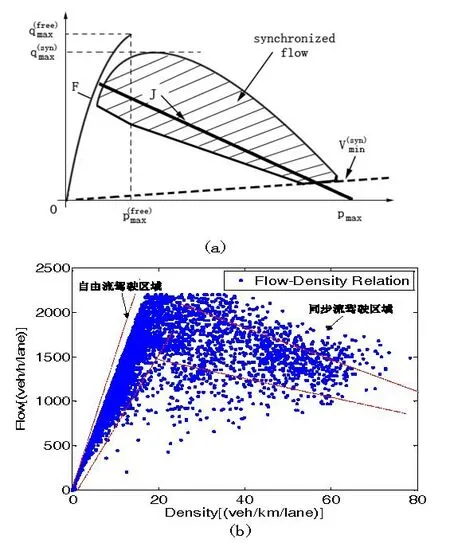
图1 三相交通流模型示意图
为了验证本文所提出的模型对三相交通流理论的还原程度,对本文模型进行仿真数值分析,Lroad为道路元胞空间,Nroad为车辆总数,虚拟道路的“流-速-密”参数的定义如式(4)~(6)所示:
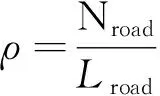
(4)

(5)
Q=ρ×Vol(veh/s)
(6)
在虚拟道路中采用周期式边界条件,每一时步的仿真完成以后都要进行边界检查。
当驾驶决策变化概率Pmax=0.5在取不同的值的时候,在对道路交通的影响分析中,随机控制参数最大加速概率Pmax=0.5;
车辆可能会应急驾驶的概率Ph=0.1,此时Ph取值较小,表示约有10%的驾驶员在发生应急状态时会急于更快的向前移动车辆,Pl=0.2表示前车受到后车的影响,也倾向于更快的移动车辆,但是模型仿真证明,这往往是交通更加恶化的主要原因,说明当应急状态出现时,即使初始时道路上车辆的车头距相对较长,道路的交通流也倾向于过渡到同步流,甚至直接发生堵塞,在本文模型中车辆随机慢化的概率Psafe=0.2。
当驾驶行为变化概率Pc分别取不同的值时,而道路密度的取值为0~1.0时,图2(a)和图2(b)分别给出了道路的“流-密”分析基本图和“速-密”分析基本图,用于分析在不同的道路密度条件下应急响应能力不同时所造成的交通流疏散能力的差异。在图2的分析中,最下方的曲线表示当Pc=0的道路基本分析图,其他的曲线表示Pc>0时的道路基本分析图。

图2 Pc参数不同取值时的基本图
可以看出在Pc=0时,反映得是应急交通响应能力不足的情况,此时道路交通很容易就会造成拥堵,当Pc>0时,说明应急交通响应能力得到了改善,同样的道路密度条件下,得到了更好的交通流,更加利于应急状态下的车流疏散。
文献[14]和文献[15]利用时间序列中的自相关性和互相关性分析提出了一种判别交通流是否处于同步流交通状态的数理统计方法,并得到了比较广泛的承认和应用,其分析流程如图3右分支所示。
通过在仿真模型的道路元胞空间中设置虚拟检测器,当车辆经过虚拟探头时也可以采集到虚拟道路中的道路交通流量、平均行车速度以及密度数据,然后对这些数据进行时间序列下的自(互)相关性分析以判定其所属的交通流状态,其分析流程图如图3的左分支所示。
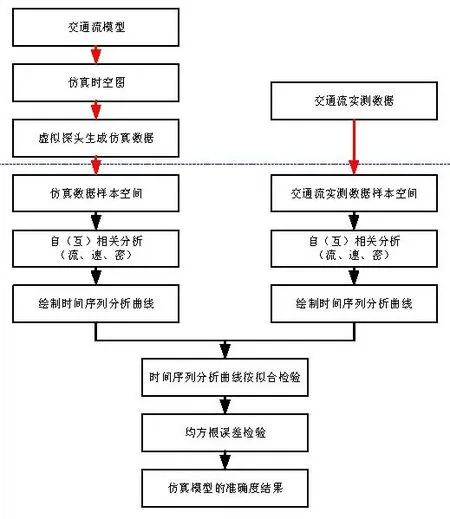
图3 三相交通流模型验证的统计分析流程
将DDM仿真模型的随机控制参数取值如下,Pchange=0.5,Ph=0.3,Pl=0.3,Pmax=0.25,Psafe=0.15,当道路密度ρ=0.6时在仿真虚拟道路上设置的虚拟检测器,以1 min的时间间隔共采样200 min的交通流样本数据(流量、速度、密度)。
首先在200 min的时长内分别进行关于流量、速度、和密度的自相关性分析,在公式(7)中a(τ)表示时间间隔为τ时的自相关系数,Xt+τ表示在相同的时间范围内,间隔为τ的表示样本的随机变量,Xt的取值可以分别为J、V、ρ,分别代表流量、速度、和密度。
(7)
分析结果得知,在τ=0时,流量、速度、和密度的自相关系数为a(0)=1,但是在长时间间隔下自相关系数在a(0)≈0附近波动,且DDM仿真模型在道路密度ρ=0.6时得到的仿真结果符合Neubert对同步流的交通状态下关于流量、速度、和密度的自相关系数的统计特征的定义。
接下来对200 min内的流量-密度的互相关性进行分析,在公式(8)中CJρ(τ)表示当时间间隔为τ时,流量-密度的互相关系数。
CJρ(τ)=
(8)
分析结果如图4所示,在同步流条件下道路密度和交通流量之间呈现弱相关性关系。在τ=0时流量-密度的互相关系数约为CJρ(0)=0.2,但是在长时间间隔下DDM仿真模型的流量-密度互相关系统在CJρ(0)≈0附近波动,所以当道路密度ρ=0.6时,关于流量-密度的互相关系数的分析也符合Neubert对同步流的交通状态下流量-密度的互相关系数的统计特征的定义,同时也证明了DDM模型符合三相交通流的理论框架。
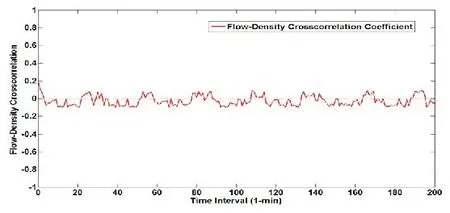
图4 同步流状态下,局部密度和平均交通流量的互相关性分析图
文献[16]曾对DDM模型进行了基本图和时空分析,为了一步与实际交通进行验证在国内某实地交通流监测点,取得所有的原始交通流检测数据,实测样本数据为隔5 min采样;
在DDM的虚拟道路上设置虚拟检测器同样以5 min的间隔获取仿真交通的数据,实测数据与仿真数据均统一为公制单位。DDM仿真模型的随机控制参数取值如下,Pchange=0.5,Ph=0.3,Pl=0.3,Pmax=0.25,Psafe=0.15,ρ=0.6。图5(a)的散点图为实测数据分析图,图5(b)的散点图为DDM仿真模型输出数据的分析图。

图5 交通流量-道路密度关系图
从图5可以看出,实测分析数据与仿真分析数据所建立的流量-密度分析图在自由流条件下时,流量与密度呈现一种递增的函数关系,但是在拥挤流状态下实测分析数据与仿真分析数据所建立的流量-密度关系弥散在一个二维区间内,符合Kerner等关于三相交通流的理论的定义。
从仿真的效果上来看,计算机机仿真模型输出数据的拟合图形呈现出比较规则的点阵,可以看出仿真的流量值区间基本上都包括实测数据的流量值的范围,仿真模型的最大仿真流量在Jmax≈2520(veh/h)左右,最小仿真流量在Jmin≈1220(veh/h)左右。
图6(a)为实测数据的速度-密度关系图,图6(b)为DDM仿真模型输出数据的速度密度关系图。仿真模型的输出图形在大体上符合实测数据的轮廓,最大仿真速度的均值在Vmax≈120(km/h)左右,最小仿真速度的均值则在Vmin≈20(km/h)左右。

图6 行车速度-道路密度关系图
接下来,对图5和图6的数值分析结果进行均方根误差检验(root mean square deviation,RMSD),然后再进行MRE检验,分别进行定量分析。对30组前后跟驰的车辆,在900 s的统计间隔内每秒钟的即时数值定义如下,θ(S)sim和θ(V)sim为仿真系统中输出的相对每秒钟的相对位移向量以及相对速度向量,θ(S)field和θ(V)field为实测的每秒钟的相对位移向量以及相对速度,如公式(9)和公式(10)所示。
(9)
(10)
则仿真值与实测交通真值的均方根误差检验的计算公式如式(11)所示,其中RMSD(θ(S)sim,θ(S)field)为仿真数据与实测交通数据的相对位移的均方根误差,RMSD(θ(V)sim,θ(V)field)为仿真数据与实测交通数据的相对速度的均方根误差:
(11)
仿真值与实测交通真值的平均相对误差检验的计算公式如式(12)所示,其中MRE(θ(S)sim,θ(S)field)为仿真数据与实测交通数据的相对位移的平均相对误差,MRE(θ(V)sim,θ(V)field)为仿真数据与实测交通数据的相对速度的平均相对误差:
(12)
表1总结了仿真值与实测交通值的拟合验证结果,从分析结果中可以看出,在900 s的时长内对30组前后跟驰的车辆的试验结果可以看出,平均相对速度与平均相对位移的均方根误差检验值(RMSD)均小于10,处于一个较低的水平内。
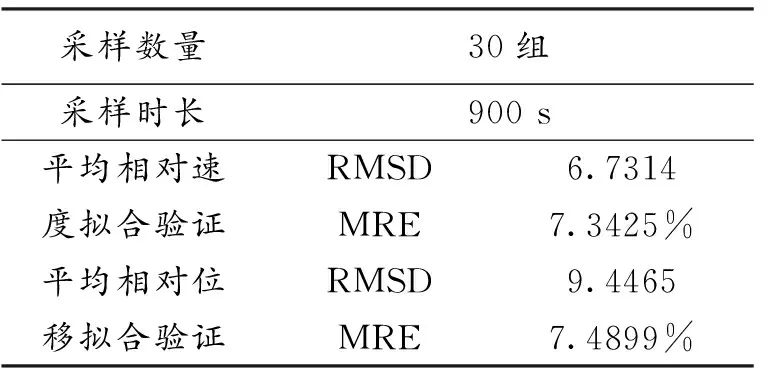
表1 仿真值与实测交通值的拟合验证结果
同时,在900 s的时长内对30组前后跟驰的车辆的平均相对速度与平均相对位移的平均相对误差值(MRE)均小于8%,也处于一个较低的水平内,从而也证明了本文仿真模型在模拟实际的应急交通流时的准确度。
本文从应急交通时交通规则实然改变时这一情景出发, 提出了DDM模型在城市交通应急疏散中的新应用模式,对模型分别进行了仿真数值分析与参数校准,数理统计分析和验证,并与真实道路的实测数据进行了拟合验证,证明了本文模型在理论框架上符合三相交通流理论,且更接近真实交通观察。
猜你喜欢交通流三相交通基于LSTM的沪渝高速公路短时交通流预测研究中国交通信息化(2022年9期)2022-10-28京德高速交通流时空特性数字孪生系统中国交通信息化(2022年5期)2022-07-23繁忙的交通童话世界(2020年32期)2020-12-25笼型三相异步电动机的起动和调速解析防爆电机(2020年5期)2020-12-14基于Motor-CAD三相异步感应电机仿真计算分析防爆电机(2020年3期)2020-11-06三相异步电动机保护电路在停车器控制系统中的应用哈尔滨铁道科技(2020年4期)2020-07-22三相异步电动机正反转的控制设计电子制作(2019年23期)2019-02-23小小交通劝导员小学生导刊(2018年16期)2018-07-02交通流随机行为的研究进展西南交通大学学报(2016年3期)2016-06-15路内停车对交通流延误影响的定量分析中国工程咨询(2016年1期)2016-02-14