董国贵 尹爱勇 董哲涵
(1.铜陵职业技术学院 安徽 铜陵 244061;
2.南通大学杏林学院 江苏 南通 226236)
开关电源由功率级电路和控制电路组成。在特定的应用场合,开关电源的功率级电路相对比较固定,为了确保开关电源正常、稳定工作,控制电路的设计和分析是至关重要的。[1]在开关电源中,电流型控制因其具有瞬态响应速度快、补偿环路易于设计,且容易实现均流、限流,已被广泛采用在各种开关电源中。峰值电流控制和谷值电流(Valley Current Mode, VCM)控制是两种常见的电流型控制。[2][3]两种控制方式不同之处在于,峰值电流控制对电感电流的峰值进行控制,而谷值电流控制对电感电流的谷值进行控制。[4]为了分析的简便,常常忽略谷值电流电压外环上的电压纹波。[5]然而,当控制环路反馈增益较大时,控制电路上的电压纹波将不可忽略,且影响谷值电流控制Buck变换器的稳定性。[6]因此,有必要深入研究控制环路对谷值电流控制DC-DC变换器稳定性的影响。
为了揭示谷值电流中存在的复杂非线性现象,国内各大院校和科研单位通过建立离散迭代映射模型研究了谷值电流控制和峰值电流控制开关DC-DC变换器间存在的对称动力学行为;
[7]还对基于谷值参考电流和输入直流电压的稳定性和分岔特性进行了分析,从而研究了谷值电流控制反激变换器的非线性现象;
[8]谷值电流模式型恒流驱动器架构从而对Buck型LED驱动器进行研究分析的众多案例等。[9]然而,关于控制环路对谷值电流控制Buck变换器稳定性影响的文献鲜见报道。为了更好地设计谷值电流控制Buck变换器,本文将开展控制环路对谷值电流控制Buck变换器稳定性影响的研究。
2.1 Buck变换器工作原理
Buck变换器是由输入电压E、开关管S、二极管D、电感L、输出电容C和负载电阻R构成的二阶电路,电路图见图1(a)。

(a)Buck变换器电路图 (b)开关状态一
当开关管S导通、二极管D关断,称之为开关状态一,如图1(b)所示;
当开关管S关断、二极管D导通,称之为开关状态二,如图1(c)所示;
当开关管S和二极管D均关断,称之为开关状态三,如图1(d)所示。在一个周期内,若电路仅存在开关状态一和二,表明开关变换器工作在电感电流连续导电模式[8](Continuous Conduction Mode, CCM);
若三种开关状态都存在,表明开关变换器工作在电感电流不连续导电模式(Discontinuous Conduction Mode, DCM)。
2.2 PI补偿VCM控制Buck变换器
PI补偿VCM控制Buck变换器的电路拓扑结构示意图如图2所示。由图2可以看出,主电路的组成为:输入电压Vg、二极管D、开关管S、输出电容C、输出电容ESR、负载电阻R;
控制电路的组成为:RS触发器、比较器、检测电阻Rs、补偿斜坡和PI补偿器,其中PI补偿器由误差放大器、补偿电容Ca和比例积分单元Ra、Rin组成。

图2 PI补偿VCM控制Buck变换器的原理图
2.3 PSIM电路建模
PI补偿VCM控制Buck变换器的PSIM仿真电路模型由主电路、控制电路、采样电路和驱动电路四部分组成,建模步骤如下:(1)搭建变换器主电路。根据谷值电流控制Buck变换器的电路拓扑结构,通过输入电压Vin(DC voltage source)、二极管D(Diode)、开关管S(MOSFET switch)、电感L(Inductor)、电容C(Capacitor)、输出电容ESR(Equivalent Series Resistance)和负载电阻R(Resistor)等元器件连接构成。(2)搭建变换器控制电路。根据变换器的工作原理,选择所需的元器件:参考电压Vref(DC voltage source)、比较器(Comparator)、时钟信号Clock(Square-wave voltage source)、补偿电容Ca(Capacitor)和比例积分单元Ra(Resistor)、Rin(Resistor)、补偿斜坡Vramp(Sawtooth-wave voltage source)和或非门(NOR gate)(用于搭建RS触发器),然后按照电路的工作原理连接好控制电路。(3)搭建变换器采样电路和驱动电路,选择电流采样元件(Current Sensor)和开关管S(MOSFET switch),通过这两个元件将控制电路与主电路连接。(4)设定仿真步长及时长和电路参数,包括电容值C(50 μF)、电感值L(100 μH)、参考电压值Vref(7 V)、时钟信号频率f(100 kHz)、负载电阻R(2 Ω)等。(5)搭建的PI补偿VCM控制Buck变换器PSIM仿真电路如图3(a)所示。

(a)添加负载跳变前 (b)添加负载跳变后
为了研究4个参数单独对PI补偿VCM控制Buck变换器瞬态性能的影响,采用控制单个参数变化的方法,基于图3(a)所示的仿真电路并在负载电阻上并联一个跳变电流源来模拟输出跳变,结果如图3(b)所示。
3.1 稳定性仿真分析
为了研究反馈增益g、输出电容ESR、输入电压Vin和补偿斜坡Vramp等4个参数对PI补偿VCM控制Buck变换器的影响。考虑到谷值电流控制技术在占空比D < 0.5时是不稳定的,设定的参考电压Vref=7 V,故设置输入电压Vin=10 V,补偿斜坡Vramp=0.01 V,输出电容ESR=10 mΩ,反馈增益g变化范围设置为5~15。以步长为1的变化来仿真分析,结果如表1所示。

表1 不同参数变化时的仿真情况
由表1可以看出,PI补偿VCM控制Buck变换器在反馈增益g较大时,存在混沌状态或不稳定的周期2状态,因此应避免反馈增益过高;
要使PI补偿VCM控制Buck变换器工作在稳定的周期1状态,应选用较小的反馈增益。在PI补偿VCM控制Buck变换器在等效串联电阻较小时,存在混沌状态或不稳定的周期2状态,因此应避免等效串联电阻过低;
要使PI补偿VCM控制Buck变换器工作在稳定的周期1状态,应选用稍大的等效串联电阻。较小的输入电压有利于PI补偿VCM控制Buck变换器工作在稳定状态。在PI补偿VCM控制Buck变换器在补偿斜坡较小时,存在混沌状态或不稳定的周期2状态,因此应避免补偿斜坡过小;
要使PI补偿VCM控制Buck变换器工作在稳定的周期1状态,应选用稍大的补偿斜坡。
3.2 不同参数平面的稳定边界
为分析以4个参数(输入电压Vin、等效串联电阻r、反馈增益g和补偿斜坡Vramp)为变量的PI补偿VCM控制Buck变换器g-r、g-Vin、g-Vramp、Vramp-r、Vramp-Vin和Vin-r的稳定边界,选择等效串联电阻r的变化范围为:10~60 mΩ,反馈增益g的变化范围为:7~14,并设定输出电压Vin为10V,补偿斜坡Vramp为0.01V进行测试,结果见图4。从图4(a)和图4(c)可以看出,在等效串联电阻r、补偿斜坡Vramp和反馈增益g较大时,变换器工作更稳定。从图4(b)可以看出,在输入电压Vin较小和反馈增益g较大时,变换器工作更稳定。从图4(d)和图4(f)可以看出,在等效串联电阻r和补偿斜坡Vramp、输入电压Vin较大时,变换器工作更稳定。从图4(e)可以看出,在输入电压Vin和补偿斜坡Vramp较小时,变换器工作更稳定。

(a)g-r平面 (b)g-Vin平面 (c)g-Vramp平面
3.3 瞬态性能仿真分析
(1)输出电容ESR的影响
为了使得变换器工作在稳定状态,选用等效串联电阻r=10 mΩ和100 mΩ作为典型波形来对PI补偿VCM控制Buck变换器的瞬态性能进行评价。减载时,如图5(a)所示,当r=10 mΩ,电压过冲的最大值为0.17 V;
当r=100 mΩ,电压过冲的最大值为0.15 V(小于0.17 V),并且二者的调整时间基本一致。因此,PI补偿VCM控制Buck变换器在减载时,等效串联电阻r越大,其瞬态性能越好。加载时,结果如图5(c)所示,当r=10 mΩ,电压跌落的极值点为A(12.0,6.50),即其电压跌落的最大值为0.50 V,电压过冲的极值点为B(12.1,7.23),即其电压过冲的最大值为0.23 V;
当r = 100 mΩ,电压跌落的极值点为A"(12.0,6.51),即其电压跌落的最大值为0.49 V,电压过冲的极值点为B"(12.1,7.15),即其电压过冲的最大值为0.15 V。在二者的调整时间基本一致,电压跌落基本一致的情况下,r=100 mΩ时的电压过冲要明显小于r = 10 mΩ时的电压过冲。因此,PI补偿VCM控制Buck变换器在加载时,等效串联电阻r越大,其瞬态性能越好。综上所述,在以上设定的参数变化范围内,无论加、减载情况,等效串联电阻r越大,PI补偿VCM控制Buck变换器的瞬态性能越好。

(a)减载时r=10 mΩ (b)减载时r= 100 mΩ
(2)补偿斜坡Vramp的影响
选用补偿斜坡Vramp= 0.01 V和0.8 V研究典型波形来对PI补偿VCM控制Buck变换器的瞬态性能。减载时,如图6(a)所示,当Vramp= 0.01 V,电压过冲的最大值为0.17 V;
如图6(b)所示,当Vramp= 0.8 V,电压过冲的最大值为0.23 V,在二者的调整时间基本一致的情况下,Vramp= 0.01 V时的电压过冲要小于Vramp= 0.8 V时的电压过冲。因此,PI补偿VCM控制Buck变换器在减载时,补偿斜坡Vramp越大,其瞬态性能越差。加载时,如图6(c)所示,当Vramp= 0.01 V,电压跌落的极值点为A(12.0,6.46),即其电压跌落的最大值为0.54 V,电压过冲的极值点为B(12.1,7.26),即其电压过冲的最大值为0.26 V;
如图6(d)所示,当Vramp= 0.8 V,电压跌落的极值点为A"(12.0,6.46),即其电压跌落的最大值为0.54 V,电压过冲的极值点为B"(12.1,7.34),即其电压过冲的最大值为0.34 V。在二者的调整时间基本一致,电压跌落一致的情况下,Vramp= 0.01 V时的电压过冲要明显小于Vramp= 0.8 V时的电压过冲。因此,PI补偿VCM控制Buck变换器在加载时,补偿斜坡Vramp越大,其瞬态性能越差。综上所述,在以上设定的参数变化范围内,无论加、减载情况,补偿斜坡Vramp越大,PI补偿VCM控制Buck变换器的瞬态性能越差。

(a)减载时Vramp=0.01 V (b)减载时Vramp=0.8 V
(3)反馈增益g的影响
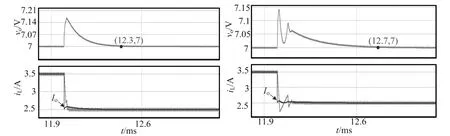
选用补偿斜坡g= 5和g= 10作为典型波形来对PI补偿VCM控制Buck变换器的瞬态性能。减载时,如图7(a)所示,当g= 5,振荡调整时间在12.3 ms时基本结束;
如图7(b)所示,当g= 10,振荡调整时间在12.7 ms时基本结束,在二者的电压过冲基本一致的情况下,g= 5时的调整时间要明显小于g= 10时的调整时间。因此,PI补偿VCM控制Buck变换器在减载时,反馈增益g越大,其瞬态性能越差。加载时,如图7(c)所示,当g= 5,电压跌落的极值点为A(12.0,6.50),即其电压跌落的最大值为0.5 V,电压过冲的极值点为B(12.1,7.2),即其电压过冲的最大值为0.2 V;
如图7(d)所示,当g= 10,电压跌落的极值点为A"(12.0,6.50),即其电压跌落的最大值为0.5 V,电压过冲的极值点为B"(12.1,7.1),即其电压过冲的最大值为0.1 V。在二者的调整时间基本一致,电压跌落一致的情况下,g= 5时的电压过冲要大于g= 10时的电压过冲。因此,PI补偿VCM控制Buck变换器在加载时,反馈增益g越大,其瞬态性能越好。综上所述,在以上设定的参数变化范围内,反馈增益g对PI补偿VCM控制Buck变换器的瞬态响应不明显。
(a)减载时g=5 (b)减载时g=10
(4)补偿电容Ca的影响
选用补偿电容Ca= 20 nF和50 nF作为典型波形来对PI补偿VCM控制Buck变换器的瞬态性能进行评价。减载时,如图8(a)所示,当Ca= 20 nF,振荡调整时间在12.4 ms时基本结束;
如图8(b)所示,当Ca= 50 nF,振荡调整时间在12.9 ms时基本结束,在二者的电压过冲基本一致的情况下,Ca= 20 nF时的调整时间要明显小于Ca= 50 nF时的调整时间。因此,PI补偿VCM控制Buck变换器在减载时,补偿电容Ca越大,其瞬态性能越差。加载时,如图8(c)所示,当Ca= 20 nF,电压跌落的极值点为A(12.0,6.50),即其电压跌落的最大值为0.5 V,电压过冲的极值点为B(12.1,7.2),即其电压过冲的最大值为0.2 V;
如图8(d)所示,当Ca= 50 nF,电压跌落的极值点为A"(12.0,6.50),即其电压跌落的最大值为0.5 V,且未产生电压过冲。在二者的调整时间基本一致,电压跌落一致的情况下,Ca= 20 nF时的电压过冲要大于Ca= 50 nF时的电压过冲。因此,PI补偿VCM控制Buck变换器在加载时,补偿电容Ca越大,其瞬态性能越好。综上所述,在以上设定的参数变化范围内,补偿电容Ca对PI补偿VCM控制Buck变换器的瞬态响应不明显。

(a)减载时Ca=20 nF (b)减载时Ca=50 nF
本文基于PI补偿VCM控制Buck变换器的拓扑结构并分析其工作原理,利用PSIM仿真软件,搭建其电路仿真模型,对PI补偿VCM控制Buck变换器进行了电路建模与仿真分析,仿真分析了PI补偿器的反馈增益、输出电容ESR、输出电压和补偿斜坡等电路参数对PI补偿VCM控制Buck变换器稳定性的影响。仿真分析表明,PI补偿VCM控制Buck变换器的稳定性会随着反馈增益g、输入电压Vin的增大而降低,随着输出电容ESR、补偿斜坡Vramp的增大而提高。此外,通过绘制6组参数平面上的稳定边界(g-r平面的稳定边界、g-Vin平面的稳定边界、g-Vramp平面的稳定边界、Vramp-r平面的稳定边界、Vramp-Vin平面的稳定边界和Vin-r平面的稳定边界)分析了输出电容ESR、补偿斜坡、PI补偿器的反馈增益和补偿电容对PI补偿VCM控制Buck变换器的瞬态性能的影响。在设定参数变化范围内,输出电容ESR越大,PI补偿VCM控制Buck变换器的瞬态性能越好;
补偿斜坡Vramp越大,PI补偿VCM控制Buck变换器的瞬态性能越差;
而在设定的参数范围内,补偿电容Ca和反馈增益g对PI补偿VCM控制Buck变换器的瞬态响应不明显。
