杨镇瑀 刘志芳
(国家开放大学,北京 100039)
对中国而言,中美利率之间的因果关系,尤其是中国利率是否会受美国利率的显著影响是一个值得持续深入探究的问题。在当前以美元为核心的国际货币体系中,对金融从业者来说,熟知美国利率是否能够影响中国利率以及在什么条件下能够影响中国利率,对不同条件下中国利率走势的预判以及相关资产的配置具有重要的指导作用;
对货币政策制定者来说,掌握中美利率关联性有利于认识美国货币政策和利率等金融条件对中国的溢出效应,从而更准确把握国内利率和流动性等金融条件的走势,进而提高本国货币政策的精准性和有效性。
实际上,对国际间利率关联性问题的研究由来已久,但关于国际间利率是否存在显著关联性的讨论并没有确定性结论。理论上,对于利率的国际关联性可从利率平价关系、三难选择、浮动恐惧、全球金融周期、两难选择、资金避风港等方面加以探讨,这些结论既有共通,又有差异。实证上,有的研究发现利率关联性与资本开放程度、汇率固定程度有关,资本完全控制或汇率完全浮动的国家可以实现本国利率自主调节;
有的发现国家间利率“短端独立、长端相关”;
有的甚至认为,除了美国外,其他国家的利率和货币政策不存在自主性;
等等。关于中美利率关联性,国内也有不少研究,研究发现其关联性与样本时间段、利率期限、中美货币政策调整策略等有关,关于中美利率彼此作用对象的结论也存在差异。无论是理论研究还是实证研究,都能加深我们对各国利率联系的认识,但其中很多研究是基于均值意义上的利率关联性,而分位数等非均值意义上的探讨则较少。鉴于此,本文采用分位数格兰杰因果关系检验来研究中美利率之间的关系,尝试利用分位数格兰杰因果关系检验的优点,揭示中美利率关联性问题中存在的“极端情形”关联现象。
(一)格兰杰因果关系的概念
自Granger(1969)提出格兰杰因果关系概念以来,格兰杰因果关系检验被广泛应用于随机变量间的因果分析。经典的格兰杰因果关系检验的基本原理是,若式(1)“几乎必然”成立,则认为x不是y的格兰杰原因,即x的过去信息不能改变y的条件分布;
反之,则认为x是y的格兰杰原因。
Fyt(Z|(,)t-1)=Fyt(Z|()t-1)
∀z∈
(1)

E(yt|(,)t-1)=E(yt|()t-1)a.s.②
(2)

E(yt|(,
(3)
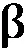
(二)分位数格兰杰因果关系检验
与均值等形式的格兰杰因果关系检验类似,分位数格兰杰因果关系检验的基本原理是:若式(4)“几乎必然”成立,则认为在分位区间[a, b]上x不是y的格兰杰原因;
反之,则认为在分位区间[a, b]上x是y的格兰杰原因。
Qyt(τ|(,)t-1=Qyt(τ|()t-1),
∀τ∈[a,b]a.s.
(4)

Qyt(τ|(,
(5)
其中,q为滞后阶数,ω(τ)、[α1(τ),α2(τ), …,αq(τ)]、[β1(τ),β2(τ), …,βq(τ)]为模型参数,参数估计值可利用分位数回归方法得到。在分位区间[a,b]上x不是y的格兰杰原因对应的原假设H0为:
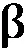
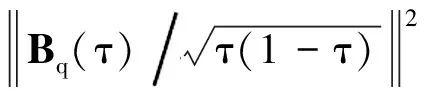
(6)
其中,Bq(τ)表示q维独立的布朗桥,‖·‖表示欧几里得范数,⟹表示弱收敛。
上述WT(τ)仅针对给定的分位点τ值,而非给定分位区间[a, b]。为检验H0在分位区间[a, b]上是否成立,Koenker和Machado(1999)、Chuang等(2009)建议采用sup-Wald方法在分位区间[a, b]上进行假设检验,即
(7)
实际操作中,在分位区间[a, b]上取n个分位点(n足够大),即a=τ1<τ2<…<τn=b,利用式(8)得到sup-Wald统计量sup WT。当统计量sup WT大于临界值c.v时,拒绝原假设H0,即认为在分位区间[a, b]上x是y的格兰杰原因。
(8)
分位区间[a, b]上sup-Wald的临界值c.v可以利用式(9)通过蒙特卡罗模拟实验得到。


(9)
其中Wq(s)表示q维独立标准布朗运动向量,s=τ/(1-τ),s1=a/(1-a),s2=b/(1-b)。与临界值c.v有关的参数有分位区间[a, b]、滞后阶数q以及显著性水平θ(一般取1%、5%和10%这三个常用数值),表1为本文的sup-Wald临界值。

表1 分位数格兰杰因果关系检验中sup-Wald模拟临界值(仅保留小数点后两位)
(一)数据说明
选用国债即期利率(连续复利率形式)来表示中美各自利率水平(后文用“利率”作为“国债即期利率”的简称)。中国利率数据来自Wind中债国债即期收益率,美国利率数据来自美联储网站“Yield Curve Models and Data—nominal U.S. yield curve”(Gürkaynak等, 2007)。分析时间段为2006年3月至2021年1月,取月末值作为每月的月度数据。选取的国债利率期限为1年、3年、5年、7年和10年④。
(二)模型说明
以式(5)为基础,在检验n年期美国利率是否是n年期中国利率的分位数格兰杰原因时,采用的分位数回归方程是:
(10)

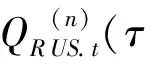
(11)

在进行分位数格兰杰因果关系检验时,选取[0.05, 0.20]、[0.20, 0.40]、[0.40, 0.60]、[0.60, 0.80]、[0.80, 0.95]这五个具有代表性的从低到高的分位区间以及[0.05, 0.95]这个总的分位区间,这几个分位区间sup-Wald统计量的模拟临界值如表1所示。在分位区间[a, b]上,回归方程滞后阶数q的选择标准为:在预设的Q(Q≤10)阶模型中,对∀τ∈[a, b],若βQ(τ)=0的原假设在分位区间[a, b]上不被拒绝,而同时βQ-1(τ)=0的原假设在分位区间[a, b]上被拒绝,则选择的模型滞后阶数为q=Q-1;
若这样的q不存在,则令q=1。整个检验过程利用R软件完成。
(三)检验结果
从检验结果看(表2),基于稳健性原则,可以得到以下几点相对稳健的结论:(1)在中国利率的低分位区间[0.05, 0.20]上,各期限的美国利率均是同期限中国利率的格兰杰原因,即美国利率能够显著影响低分位区间同期限的中国利率。(2)在中间分位区间[0.40, 0.60]、[0.60, 0.80]上,各期限的中美利率之间没有显著统计关系。(3)在选取的所有分位区间上,各期限的中国利率几乎均不是同期限美国利率的格兰杰原因,即中国利率几乎不能显著影响同期限美国利率,可以认为中美利率之间存在单向的格兰杰因果关系。

R(7)19.43∗∗[2]0.76[1]0.32[1]0.15[1]2.33[1]4.12[1]R(10)3.51[1]0.46[1]0.28[1]0.31[1]12.03∗∗[2]4.71[1]
从系数估计值符号(图1)看,以1年期的β1(1)(τ)为例,在低分位区间[0.05, 0.20]上,美国利率对中国利率的作用方向为正,即在低分位区间[0.05, 0.20]上,美国利率下降(或上升)会引起中国利率水平降低(或增加)。值得注意的是,若采用最小二乘法LS进行回归估计,系数β1(1)将不显著,而若采用分位数回归,系数β1(1)(τ)在分位区间[0.05, 0.20]上显著为正,这意味着分位数回归可以识别出均值回归不能识别出的信息,尤其是尾部区间的信息。

图1 分位区间[0.05, 0.20]内β1(1)(τ)(q=1)的估计结果⑤
(四)结果分析
国债利率的低分位区间通常对应着“经济遭受极端的负向冲击”,如2008年国际金融危机和2020年新冠肺炎疫情危机。这意味着从危机的角度思考上述结果会是一个合适的切入点:第一,危机期间,全球经济“同舟共济”,中美等全球经济关联性增大,此时中美等国货币政策协调性高,体现为中美利率正向关联性强。例如,在2008年国际金融危机期间,全球主要国家加强货币政策、财政政策等宏观政策的协调与对话,以共同应对国际金融危机对本国经济的巨大负向冲击。第二,从金融市场的角度看,危机期间不确定性高,美国国债常被视为资金避风港,往往会出现资金从其他国家向美国大量流动的现象。为缓解国内流动性缺失和风险溢价的上升,其他国家不得不向市场提供足够的流动性,降低无风险利率,以保持国内货币和金融市场的稳定,进而表现为美国国债市场对其他国家货币和金融市场的影响。第三,不容忽视的是,为了应对国际金融危机和新冠疫情危机,美联储在联邦基金利率降至零下界后,不得不采用量化宽松等非常规货币政策,通过购买中长期国债等资产向市场注入大量流动性,这些流动性存在明显的外溢现象,成为中国利率变动的一个重要原因。美国利率是中国利率低分位区间的单向格兰杰原因能够在一定程度上说明美国量化宽松政策对中国金融市场存在单向的外溢效应。
无论是自建、共建、公建还是商建,都必然涉及住房用地制度、住房金融制度、住房产权制度(住房产权结构、住房产权的覆盖面:全覆盖、半覆盖和零覆盖)以及相关政策等。因此,城镇住房供给制度是本文研究的主要内容。
综合而言,表2的结果表明,美国利率在“极端情况下,尤其是在全球极端负向冲击情况下”会是引起中国利率发生变动的显著原因。相反,几乎在所有情况下,中国利率都不是美国利率发生变动的原因。这也与现实的情况相符,因为美国作为全球的金融中心以及美元作为全球货币体系的核心货币,其货币政策和利率水平能够对其他国家的利率、流动性以及货币政策等有较大影响,相反,其货币政策和利率受其他国家的影响则较小⑥。
本文利用分位数格兰杰因果关系检验分析了中美利率之间的关系,发现美国利率能够显著影响中国低分位区间的利率水平,但不能显著影响中国中间分位区间的利率水平。与此同时,中国利率对美国利率水平没有显著影响,即中美利率之间的互动关系表现为美国利率影响中国低分位区间利率这一单向格兰杰因果关系。这说明美国利率对中国利率有显著影响,但这种影响是有条件性的,因此在分析美国利率对中国利率的影响时,应该视情况而定。既然中国利率水平既会受美国利率一定影响,又会对美国利率保持一定自主性,且这种“受影响”和“自主性”的表现条件有所区别,即“受影响”表现在“极端条件”下,而“自主性”表现在“正常条件”下,可考虑如下建议:
一是从具体的利率预判上看,在危机、量化宽松等非常规的“极端”情况下,应该特别重视美国利率及其货币政策立场等美国因素,而在利率位于适中区间时,应转而重点关注国内经济金融条件、国内货币政策等国内因素,提高研判的有效性。二是从国内政策含义看,中国的货币政策等宏观政策在考虑外部因素以及本国政策自主性时,应该视情况而定:在面对较大极端性冲击尤其是全球极端负向冲击时,中国货币政策的实施应该考虑美国货币政策立场及其实施策略,注重全球货币政策的协调性;
而在经济运行平稳、经济不遭受重大负向冲击、利率回到适中水平时,本国货币政策可以更多考虑“以我为主”的政策基调。
[注 释]
①因此,采用式(1)分布形式的格兰杰因果关系可被称为分布格兰杰因果关系。显然,均值、方差、VaR等形式的非格兰杰因果关系仅是分布非格兰杰因果关系的必要条件。
②a.s.表示“几乎必然”,是almost surely 的缩写。
④由于自2008年11月以来,美国联邦基金利率长时期处于零下界附近,期限较短的美国国债利率变动空间有限,因而并不能较好反映有关美国货币政策的新信息;
而期限较长的国债利率能较好反映美国货币政策的新信息(Gertler和Karadi,2015)。
⑤横轴为分位数,纵轴为系数值。水平实线表示系数的LS估计值,水平虚线表示LS估计值95%置信区间的上界。点状曲线表示系数的分位数回归估计值,阴影部分表示分位数回归估计值95%的置信区间。
⑥尽管当前中国已是全球第二大经济体,但由于人民币在国际结算中的占比仍旧远远低于美元、中国对资本流出的管制力度高于美国、中国货币政策一直处于正常化阶段而没有产生如量化宽松政策般的流动性溢出等原因,中国的利率、流动性等金融因素对美国货币政策和利率的影响尚不具有较大的影响。但随着中国经济全球占比持续提升、人民币国际化持续推进、资本对外开放程度不断深化等因素的发展,中国货币政策、利率等金融因素将可能对全球乃至美国的影响程度有所提高。
猜你喜欢格兰杰位数关联性基于单元视角的关联性阅读教学策略浅探小学教学参考(语文)(2022年3期)2022-05-26学贯中西(4):AI的时序性推论技能电子产品世界(2022年2期)2022-03-22燃气热水器性能与关键结构参数关联性分析煤气与热力(2022年2期)2022-03-09比较小数的大小小学生学习指导(中年级)(2020年3期)2020-01-03《两位数除以一位数笔算除法》教学设计学校教育研究(2019年24期)2019-02-07国内外铜期货市场的格兰杰因果检验分析中文信息(2017年3期)2017-05-22进出口贸易对我国城镇化发展的影响商业经济研究(2016年7期)2016-04-19比大小有窍门读写算·小学低年级(2015年3期)2015-12-04临终的医生与关怀的本意中国新闻周刊(2014年5期)2014-02-17叶丽娅的年龄读者·校园版(2013年10期)2013-05-14