郭广思,王 亮,杜晓明,李 宁
(沈阳理工大学 材料科学与工程学院,沈阳 110159)
7075铝合金具有良好的抗应力腐蚀性能,其刚度和强度高、不易断裂、疲劳极限高,广泛应用于交通、兵器、航天等领域[1-3]。然而7075铝合金存在韧性差、凝固温度区间大、偏析严重、热裂倾向大、力学性能在高温下明显降低等问题[4],限制了其进一步发展和应用。
石墨烯具有优良的力学及其他物理性能,其独特的二维结构及纳米级尺寸使其可以作为理想的增强体强化7075铝合金,相较于传统的增强体材料,纳米级石墨烯电子迁移率高[5]、热膨胀系数低、导热导电性好。近年来,国内外学者对石墨烯增强铝基复合材料的制备技术、增强机理、力学性能及导热性能等进行了大量研究。燕绍九等[6]以石墨烯为增强相、铝合金粉末(镁、铜含量分别为1.5%和3.9%)为基体,制备了石墨烯质量分数为0.3%的铝基复合材料,测试结果表明材料抗拉强度提高了25%、屈服强度提高了58%、断裂伸长率提高了7%。Wang等[7]以0.3%的石墨烯作为增强相,以球形铝粉(直径约10 μm,纯度99%)经球磨转化的2 μm厚铝片为基体,制备了铝基复合材料,其抗拉强度提高了62%。Yan等[8]以0.5%的片状石墨烯增强铝合金微粒,制备了铝基复合材料,其屈服强度提高了22.4%。
由于石墨烯的加入,复合材料在加工过程中易造成缺陷,形成孔洞、杂质等,这些部位会成为断裂时裂纹的潜在起点,其可加工性能变差[9]。目前对石墨烯增强铝基复合材料的高温变形行为研究较少[10],为优化变形加工参数,改善其热加工性能,本文对石墨烯增强7075铝基复合材料进行热压缩变形实验,研究应变速率和变形温度对材料热压缩流变应力的影响,并根据实验结果建立各参数之间的双曲正弦型本构方程。
1.1 实验材料
实验材料为镀铜石墨烯增强7075铝基复合材料,采用真空热压烧结技术制备而成,石墨烯质量分数为0.5%。复合材料的制备及热处理细节详见文献[11]。采用线切割将复合材料样品切割成φ8 mm×12 mm的圆柱,作为热压缩试样备用。
1.2 热压缩实验
热压缩实验设备为MMS-100热模拟实验机(东北大学RAL国家重点实验室研发生产)。实验样品以10℃/s的升温速率加热至设定温度,并保温3 min,确保样品受热均匀。压缩过程为等温单道次压缩,试样压缩量为总长度的60%,压缩完成后淬火处理。热压缩实验中试样温度T分别取为300℃、350℃、400℃、450℃,应变速率̇ε分别为0.001 s-1、0.01 s-1、0.1 s-1、1 s-1。由MMS-100热模拟实验机自动采集实验数据,包括压力、温度、位移、真应变、真应力、时间等,并绘制真应力-真应变曲线。
2.1 热压缩变形真应力-真应变曲线
温度分别为300℃、350℃、400℃、450℃时,石墨烯增强7075铝基复合材料在不同应变速率̇ε下的真应力-真应变曲线如图1所示。
由图1可见,变形温度、应变速率及应变是影响流变应力的主要因素。在同一应变速率下,变形温度升高,流变应力降低;
在同一变形温度下,应变速率增大,流变应力增加。在热压缩变形初期,应力随应变的增加迅速增大,达到上屈服极限,此时为加工硬化阶段,试样发生弹性变形;
随着应变量继续增加,晶粒中位错开动,应力迅速降低;
随后在相当大的应变范围内,材料内部同时发生动态回复与加工应变硬化作用,动态回复使铝合金软化,应力-应变曲线下降,加工硬化使铝合金硬化,应力-应变曲线上升,二者交互作用使曲线出现锯齿状波动;
某些温度和应变速率(如温度300℃、应变速率0.001 s-1)条件下加工硬化与动态回复作用接近平衡,加工硬化率趋于零,曲线出现水平阶段,即应力不随应变而变化的稳定状态[12]。

图1 不同变形条件下的真应力-真应变曲线
2.2 热压缩变形本构方程
为阐明石墨烯增强铝基复合材料在热压缩下各影响因素之间的关系,构建流变应力σ与热变形参数(和T)之间的本构关系。
流变应力σ、应变速率和变形温度T在不同的应力水平下分别满足不同的关系式,广泛使用的是Arrhenius型本构方程,其包括幂函数、指数及双曲正弦三种形式[13],具体如下。
适于低应力水平(ασ<0.8)的幂函数形式为

适于高应力水平(ασ>1.2)的指数形式为

适于全部应力范围的双曲正弦形式为

式中:Q为变形激活能;
R为气体常数;
α、β、A、A1、A2、n、n1为材料参数,与温度无关。式(1)~(3)之间具有一定的关联性,材料参数α、β与n1之间满足如下关系。

以图1中应变为0.1时对应的实验数据为例,确定式(1)~(3)中的未知参数。图1中应变为0.1时不同温度和不同应变速率对应的应力如表1所示。
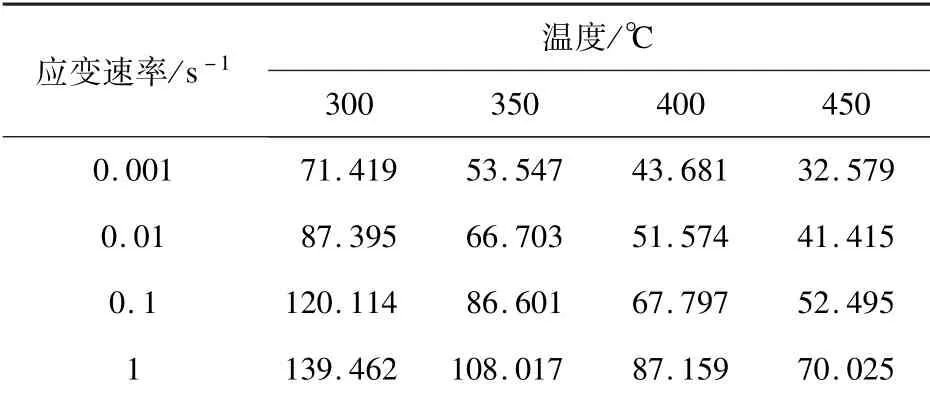
表1 应变为0.1时不同条件下材料的应力MPa
将式(1)和式(2)两边分别取自然对数得
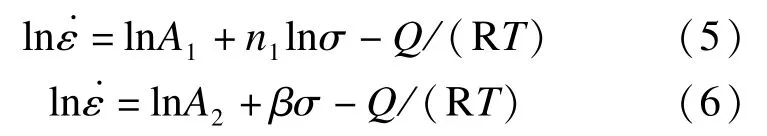
将表1中400℃、450℃下应力(视为低应力水平)及与其相对应的应变速率代入式(5),300℃、350℃下应力(视为高应力水平)及与其相对应的应变速率带入式(6),分别作ln-lnσ和ln-σ散点图,并对散点图进行线性拟合,结果如图2和图3所示。
由式(5)和式(6)可知,图2和图3中ln-lnσ、ln-σ拟合直线的斜率分别为n1和β。取图2和图3中不同温度下直线斜率的平均值,得到n1和β的值分别为9.396和0.109 MPa-1,进一步由式(4)计算得到α=0.0116 MPa-1。
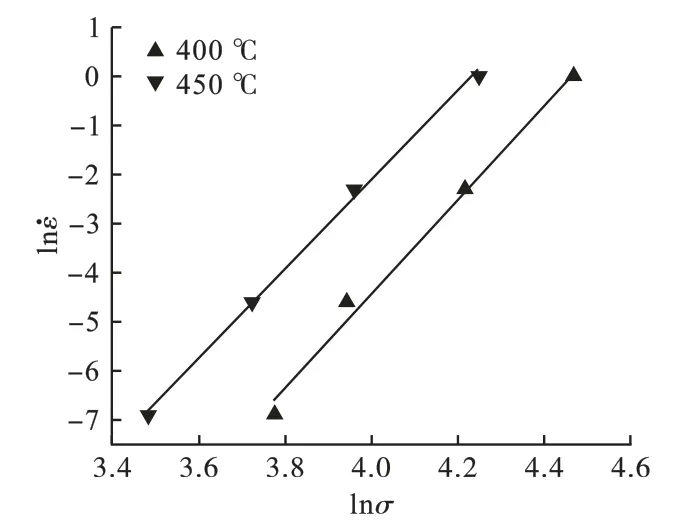
图2 不同温度下ln-lnσ的线性拟合

图3 不同温度下lṅε-σ的线性拟合
对式(3)两边分别取自然对数得

将已得到的α值及表1中不同温度下应力与对应的应变速率代入式(7),作lṅε-ln[sinh(ασ)]散点图,并进行线性拟合,结果如图4所示。

图4 不同温度下lṅε-ln[sinh(ασ)]的线性拟合
图4中直线的斜率即为应力指数n,取图4中不同温度下直线斜率的平均值,得到n=7.721。
在应变速率一定的情况下,将式(7)两边对(1/T)求偏导可得

作不同应变速率下的ln[sinh(ασ)]-1/T散点图,并进行线性拟合,结果如图5所示。
由图5可以看出,ln[sinh(ασ)]-1/T较好地满足线性关系,即石墨烯增强铝基复合材料在300~450℃变形时的流变应力方程较好地符合双曲正弦函数形式。由式(8)知,图5中拟合直线的斜率即为Q/(Rn),取图中不同应变速率下直线斜率的平均值得Q/(Rn)=2.602,将n值代入,求得Q=167.029 kJ/mol。

图5 不同应变速率下ln[sinh(ασ)]-1/T的线性拟合
由式(7)可知,图4中拟合直线的截距为[lnA-Q/(RT)],根据截距数值,将Q值代入,计算得到各温度下的A值,取平均值得到A=2.331×1012s-1。
将上述得到的所有参数代入式(3),即可得到应变为0.1时石墨烯增强铝基复合材料的Arrhenius型双曲正弦函数本构方程。
上述本构方程的相关运算是在应变量一定的前提下,考虑温度和应变速率对石墨烯增强铝基复合材料流变应力的影响。为获得更加精确的本构方程表达式,进一步考虑应变对流变应力的影响。按照上述在真应变为0.1时确定双曲正弦本构方程中参数α、n、Q、A的过程,依次确定真应变ε分别为0.2、0.3、0.4、0.5、0.6时的材料参数,结果如表2所示。
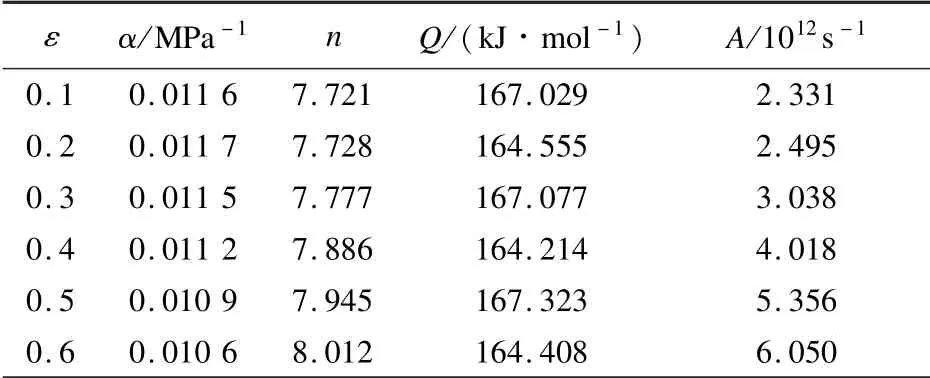
表2 不同应变下本构方程中α、n、Q、A的值
按照表2数据,对α、n、Q、A和ε之间的关系进行非线性拟合。根据散点图分布规律,α-ε采用二次函数模型、n-ε与A-ε采用一次函数模型、Q-ε采用三角函数模型,拟合结果如图6所示。
图6中各拟合关系式分别为

图6 变形激活能及各材料参数与真应变的数据拟合


由图6可见,各参数拟合效果良好。拟合度均达到98%以上。
将式(9)~(12)代入式(3)即可得到由温度、应变速率和应变等变形参数表达的石墨烯增强铝基复合材料高温热变形本构方程。
取三组不同温度和不同应变速率下的真应力实验数据对上述本构方程进行验证,结果如图7所示。
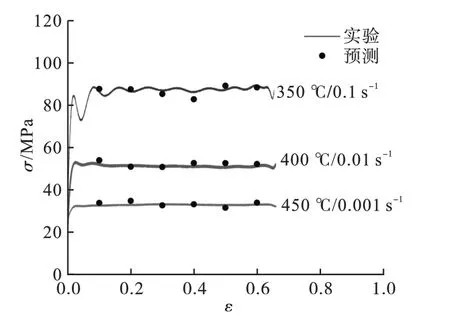
图7 热变形本构方程预测流变应力与实测流变应力比较
由图7可见,采用本文所确定的本构方程计算不同条件下的应力,预测数值与实验值吻合较好,最大误差为4.8%。在本文给定的变形条件(应变速率0.001~1 s-1,温度300~450℃)下,本构方程拟合精度较高。
(1)石墨烯增强铝基复合材料的流变应力随应变的增加先迅速增大,当达到峰值应力后略有下降,并出现锯齿状波动,部分曲线出现稳态流变特征。
(2)在温度为300~450℃、应变速率为0.001~1 s-1的条件下,确定了以温度、应变速率和应变等变形参数表达的石墨烯增强铝基复合材料双曲正弦本构方程,经该本构方程计算的流变应力与实验值误差小于4.8%。本文确定的本构方程能够很好地描述石墨烯增强铝基复合材料的热变形行为。
猜你喜欢双曲本构石墨一类双曲平均曲率流的对称与整体解数学物理学报(2022年4期)2022-08-22石墨系升温球的实践与应用昆钢科技(2022年1期)2022-04-19中国科学技术馆之“双曲隧道”军事文摘(2021年22期)2022-01-18双曲型交换四元数的极表示华东师范大学学报(自然科学版)(2020年1期)2020-03-16离心SC柱混凝土本构模型比较研究工程与建设(2019年3期)2019-10-10锯齿形结构面剪切流变及非线性本构模型分析西南交通大学学报(2018年5期)2018-11-08一种新型超固结土三维本构模型潍坊学院学报(2017年2期)2017-04-20石墨烯在超级电容器中的应用概述通信电源技术(2016年6期)2016-04-20基于双曲和代数多项式的HC-Bézier曲线湖南城市学院学报(自然科学版)(2016年4期)2016-02-27石墨矿中固定碳的分析与探讨中国非金属矿工业导刊(2014年3期)2014-02-28