王永贵,张 鉴
辽宁工程技术大学 电子与信息工程学院,辽宁 葫芦岛 125105
推荐系统是一种优秀的信息过滤器,它能够迅速而准确地找到用户所需数据,有效缓解信息超载问题,是目前最受欢迎的研究领域之一[1]。推荐系统可分为两类,分别是生成个人推荐的个性化推荐系统和提供组推荐的群组推荐系统,在这两者之间,个性化推荐在技术和应用方面已非常成熟,然而在很多情况下推荐系统需要为群组提供推荐,如家庭聚餐、旅行团兴趣点以及其他娱乐目的等活动需要考虑群组内所有成员的偏好进行推荐。因此,群组推荐系统正在受到越来越多的关注,并逐渐成为学术界的研究热点之一[2]。
与面向个人的推荐不同,在群组推荐中,推荐结果需要使绝大多数组成员对推荐结果感到满意,而群组推荐的结果是基于对单个用户的偏好拟合和所有用户的偏好融合[3]。
对于单个用户偏好的拟合,常用的方法是将个性化推荐技术应用到群组推荐中。协同过滤是当前个性化推荐技术中应用最为广泛、发展最为成熟的个性化推荐技术之一[4]。它利用兴趣相投、喜好相似的群体的偏好来推荐用户感兴趣的项目与信息,通过个人所给予信息的反馈记录达到过滤的目的,从而帮助其他人来筛选信息。例如,陆航等人[5]提出了一种融合用户兴趣和评分差异的协同过滤推荐算法,将用户兴趣相似性和评分差异相似性进行加权融合,获取更加准确的用户邻居,从而预测项目评分并进行推荐,能够有效缓解单一评分相似性计算不准确的问题且具有良好的可扩展性,但是当面对大规模数据集或稀疏数据集时,算法表现较差。为了解决这些问题,概率矩阵分解(probabilistic matrix factorization,PMF)方法被提出,它是一种流行的基于模型的协同过滤方法,该方法通过将评分矩阵分解为两个低维潜在因子矩阵,并使其乘积接近评分矩阵,从而预测未知评分,具有准确和稳定的预测性能,并且可以利用边信息来有效缓解数据稀疏和冷启动问题[6]。但是,PMF方法在计算过程中忽略了用户之间的关系信息,而用户之间的交互关系往往会对用户的偏好产生较大影响,预测结果的准确性仍有待提高。本文提出了联合用户关系的概率矩阵分解算法,在经典概率矩阵分解算法中加入了用户关系信息,具有更好的偏好拟合效果。
完成单个用户的偏好拟合后,群组推荐中的另一个问题是群组成员偏好的融合,完成融合的方法有两类,分别是模型融合方法(PA)和推荐融合方法(RA)。PA方法是将组用户的偏好转化为整个群组的偏好,然后将整个群组作为虚拟用户,通过个体预测模型计算预测值。换句话说,这种方法在预测所有项目的评分之前,为整个群组构建一个偏好模型。例如,杨丽等人[7]提出了一种基于ranking的混合深度张量分解群组推荐算法,基于成对张量分解模型来捕获群组偏好模型,有效提高了推荐效率,但是由于一些特殊群组成员的意见可能会被忽略使得整个群体的偏好无法有效地代表;
毛宇佳等人[8]提出了一种缩小群组推荐列表的方法,该方法通过划分子组来缩小群组规模并减少群组偏好属性数量,保证了推荐的公平性,具有较好的群组推荐效果,但是在数据集稀疏的情况下,由于缺乏大量原始评级信息,构建群组偏好模型的能力较差,数据越稀疏,融合越困难;
Ding等人[9]提出了一种基于模糊聚类的随机群推荐模型,通过分析组中所有用户的项目评分,推荐模型可以将群组抽象为虚拟用户,然后应用个人推荐算法为虚拟用户推荐前K个最吸引人的项目,并采用偏好评分和基于多类的模糊聚类算法对群推荐模型的推荐结果进行优化,与传统的群组推荐相比,该群组推荐模型推荐的项目用户满意度更高,但是付出了多样性和公平性方面的代价,导致推荐精度不高,并且在大规模群组内算法准确度仍有待提高。总而言之,对于PA方法,它只是简单地合并用户偏好构建群组模型,这种做法并不严格,因为一些特殊群组成员的意见可能会被忽略,整个群组的偏好无法有效地代表。
群组推荐的另一种方法是RA方法,该方法首先为每个组成员生成预测,然后将这些预测合并为最终群组推荐结果。它有两个主要分支,分别是基于预测评分的推荐融合方法(PRA)和基于推荐列表的推荐融合方法(RRA)。PRA方法汇总了各组成员对一组中所有项目的预测评分,并将其作为该组对相应项目的预测评分,RRA方法则是将每个组成员的排名列表融合为整个群组的最终排名列表。
对于RRA方法的研究,李晓鹏等人[10]提出一种基于MedRank排序算法的群组推荐方法,该方法顺序访问每个群组用户排序列表,通过顺序排序算法输出最终的群组推荐列表,这种方式可以避免当群组规模扩大时,群组推荐结果满意度降低现象的产生,但是未考虑项目的具体排名信息,推荐精度较低;
Du等人[11]提出了一种基于学习排序算法的群体活动推荐框架,使用贝叶斯群组排序算法将每个组成员的排名列表融合为整个群组的最终排名列表,该方法可扩展性强,但是同样未考虑项目的具体排名信息,导致不精确的组排名列表。总而言之,由于RRA方法只使用排名信息,而不知道列表中两个推荐项目的差异细节,可能会导致不精确的群组排名列表。相反,利用预测值进行融合的PRA方法可以被视为更具体、更准确的群组推荐方法。因此,本文的研究主要集中在PRA方法上。
对于PRA方法的研究,Liu等人[12]提出了一种基于群内发散协同过滤的群组推荐方法,考虑用户对时间和项目类别的偏好构建用户偏好向量,然后建立群体特征得到群组与其他用户特征偏好的相似度,最后基于群体内散度计算群组的偏好评分,该方法适合为大规模群组推荐,但是当群组规模较小,用户偏好不足时,推荐效果会很差;
叶柏龙等人[13]提出了一种基于评分与项目特征相结合的方法,通过计算群组在项目特征和评分上的综合相似度进行预测评分并产生推荐,该方法可以考虑每个成员与项目之间的关系,但数据的稀疏性影响推荐结果;
杨金劳等人[14]提出了一种基于改进矩阵分解的群组推荐算法,首先根据用户共有群信息计算用户间的相关性并将其集成到矩阵分解中以生成单用户的偏好评分,然后采用基于均值与最小辛苦策略融合的修正满意平衡策略进行评分融合,该算法能够考虑到用户与群组之间的关系,但是忽略了个别影响力因子大的用户对整个群组的影响,且在大规模的群组中推荐的满意度与准确率偏低;
尹青山[15]提出一种基于改进矩阵分解的群组推荐算法,以融入群组特有信息的矩阵分解为基础模型生成群内单用户的偏好评分,然后采用群推荐中传统融合策略进行个人评分融合,该方法能够很好地获取个人预测评分,但是在群组偏好融合的过程中使用传统融合策略只是简单地将群组内所有成员的评分进行合并,未考虑用户权重应不同,偏好融合效果欠佳;
Guo等人[16]提出了一种基于偏好关系的群组推荐模型,使用多元回归和极端学习程序预测每个用户的预测评分,偏好融合则使用borda规则实现,实验表明该模型适用于大规模群组推荐,缓解了群组推荐的数据稀疏性问题,但是borda规则是传统融合策略的一种变式,偏好融合表现较差,导致推荐的准确度较低。
综上可知,群组推荐方面的研究虽然众多,但是仍然存在以下方面需要进一步研究:一方面是对于单个用户的偏好拟合,概率矩阵分解虽然具有稳定的预测性能,并且可以利用边信息来有效缓解数据稀疏问题,但是在计算过程中忽略了用户之间的关系信息,而用户之间的交互关系往往会对用户的偏好产生较大影响,因此预测结果的准确性仍有待提高;
另一方面是对于群组用户的偏好融合,当群组成员之间存在偏好冲突时,传统融合策略无法提供良好的群组推荐,而且将相同的权重分配给组中的所有个体,不能反映不同组用户在实践中的实际贡献。事实上,群组中所有成员都应该有不同的影响,在群组中有重要地位或能够为群组做出更多贡献的人,在偏好融合的过程中应该拥有更高的权重,而且考虑到在群组中会有一些不可靠成员随意评分,可能导致不准确的推荐结果,用户的可靠性也是一个必须考虑的因素。
为解决上述问题,本文提出了融合概率矩阵分解与ER规则的群组推荐方法(FPMF-ER),该方法通过联合用户之间的关系信息对经典概率矩阵分解算法进行改进,不仅能够有效缓解数据稀疏问题,而且能够获得更加准确、完整的单个用户预测评分,为后续群组推荐工作奠定良好的基础;
随后,在群组成员偏好融合的过程中引入ER规则,利用ER规则合理地将权重和可靠性分配给不同的群组成员,保证了冲突偏好之间的准确融合,能够更加真实合理地反映偏好融合的过程。本文的主要贡献可概括如下:
(1)提出了一种融合概率矩阵分解与ER规则的群组推荐方法,有效提升了群组推荐系统性能;
(2)在单个用户偏好拟合阶段,联合用户关系信息对PMF方法进行改进,提出联合概率用户关系的概率矩阵分解方法,以获取更完整、更准确的单个用户偏好拟合结果;
(3)在群组偏好融合阶段,提出一种基于ER规则的偏好融合方法,通过ER规则根据群组成员的权重和可靠性识别群体成员的重要性和影响力,使偏好融合过程更加科学合理;
(4)为了评估所提出的群组推荐方法的性能,在Book-Crossing数据集上进行了对比实验,实验结果证明了所提出方法的有效性。
在本章中,使用联合用户关系的概率矩阵分解方法获取完整且准确的个人预测评分,完成单个用户偏好的拟合。拟合过程分为两步:首先,构建用户关系矩阵,并通过经典概率矩阵分解算法对用户关系矩阵进行补全;
随后,将补全后的用户关系矩阵和用户-项目评分矩阵引入改进后验概率的概率矩阵分解获取个人预测评分。
1.1 构建用户关系矩阵
对于群组中的用户,根据公式(1)计算得到用户之间的关系信息,并将关系信息储存在一个M×M维的矩阵S中,M表示用户数量,矩阵的元素Sl,r表示用户l和用户r之间的关系信息。
其中,rl,i、rr,i分别表示用户l对项目i的评分和用户r对项目i的评分;
、分别表示用户l的平均评分和用户r的平均评分。Sl,r的值在−1到+1之间,值越接近1,表示两个用户之间的关系越紧密。
但是,由于关系信息是基于评分信息得到,而一般情况下用户倾向于只对大量项目中的少数进行评分导致数据稀疏,所以需对关系信息进行补全。
假设关系信息矩阵S是由用户l的潜在向量L和用户r的潜在向量R的内积来决定,且服从高斯分布,如式(2)所示:
则关系信息矩阵的条件分布可表示为如式(3)所示,其中Il,r为指标函数,如果用户l与用户r之间存在关系信息值,则为1,否则为0。
再假设,用户l的潜在向量L和用户r的潜在向量R都服从均值为0的高斯分布,即:
则对于用户l的潜在向量L和用户r的潜在向量R,其后验分布的对数函数如式(6)所示。其中,C是一个不依赖参数的常量。
最大化后验分布的对数函数等价于最小化含有二次正则项的平方误差和的目标函数,目标函数如式(7):
最后,目标函数E分别对Ll、Rr求导,如式(8)、式(9)所示:
迭代更新完成后,用户l和用户r的关系可通过Ll与Rr相乘取得,从而获得补全后的关系信息矩阵F,且矩阵F的第r行表示用户r与其他用户之间的关系信息。
1.2 获取个人预测评分
假设在一个群组中有M个用户和N个项目,形成一个M×N维的用户-项目评分矩阵R,矩阵的元素Ri,j表示用户i对项目j的评分值。
再假设评分矩阵R是由用户潜在向量U(M×D)与项目潜在向量V(N×D)的内积求得,且服从均值为,方差为的高斯分布,其中D是潜在特征矩阵,则矩阵R的概率分布如式(10)所示:
在1.1节中,经过计算得到补全后的用户关系信息矩阵F,根据式(11)对矩阵F的每行值进行归一化。
则用户i的潜在向量Ui可表示为矩阵F中其他用户的潜在向量乘以权重求和得到,如式(12)所示:
于是,用户潜在向量U的高斯先验分布如式(13)所示,项目潜在向量V的高斯先验分布如式(14)所示:
则对于用户潜在向量U和项目潜在向量V,其后验分布的ln对数函数如式(15)所示:
而最大化该后验分布的对数函数,等价于最小化含有二次正则项的平方误差和的目标函数L,如式(16)所示,其中λU=σR2/σU2,λV=σR2/σV2,λF=σR2/σF2。
最后,目标函数L分别对Ui和Vj求导,如式(17)、式(18)所示:
在计算潜在特征向量后,获得值=UiTVj,其中表示用户i对物品j的预测偏好得分。至此,形成补全后的用户-项目评分矩阵R,并获得每个单个用户对所有项目的预测值,将用于为后续偏好融合阶段做准备,是群组偏好融合过程中的重要组成部分。
2.1 群组推荐过程
本文在群组偏好融合的过程中引入ER规则,它是一种多准则决策分析的通用方法,使用统一的信念结构来建模各种类型的不确定性,可以被视为一种概率方法,并充分利用所有用户生成的数据,属于人工智能范畴,常用于信息融合、专家系统、多准则决策分析等方面。ER规则通过合理地分配证据的权重和可靠度,使得证据在不同的决策场景中具有与之相适应的特性,保证了高冲突证据之间的准确融合,而且它在计算过程中采用正交和算子进行证据组合,通过迭代计算,大大减小了传统证据组合的计算量,避免了组合爆炸问题[17-20]。
基于ER规则的偏好融合方法细节描述如下:在第1章中获得了完整的用户-项目评分矩阵R,可以显示各组成员对项目的预测值,群组中的每个用户对项目的预测值都可以作为一个证据用来预测整个群组的真实偏好,通过ER规则识别每个用户权重以及可靠性,然后将所有用户的预测值融合生成群组对项目的预测值,最终得到群组的推荐结果。基于ER规则的偏好融合方法的工作原理如下。
定义1(识别框架)对于一个群组,认为项目集合Θ={v1,v2,…,vN}一个识别框架,其中Θ是一组相互排斥且详尽的待推荐候选项目,识别框架的vj代表第j个项目。此外,Θ的所有子集构成幂集p(Θ),如式(19)所示:
定义2(证据)证据ei由信任分布来表示,如式(20)所示:
其中,(v,pv,i)表示支持假设v的证据,其概率为pv,i,由群组中第i个成员形成,概率pv,i由群组成员对项目的预测值表示,这里v可以是除空集之外Θ的任何子集或p(Θ)的任何元素。
定义3(权重和可靠性)假设wi(0≤wi≤1)和Ri(0≤Ri≤1)分别是任意用户i的权重和可靠性,wi表示用户i的重要程度,越接近0表示越不重要,越接近1表示越重要,Ri表示用户i的可靠程度,越接近0表示越不可靠,越接近1表示越可靠。
若某个用户在一个群组中有重要的位置,或者可以为推荐工作做出更多的贡献,那么他的权重应比较高。一般情况下,为了使推荐结果尽可能地满足群体的偏好,所有用户都对同一个目标做出了贡献,而某个用户的推荐召回率越高,说明这个用户可以从群组的实际偏好中取回更多的项目,同时也说明这个用户对社群的贡献越大,因此将用户的推荐召回率作为权重,用户i的权重设置如式(21)所示:
其中,Qt表示用户i正确推荐项目的数量,Q表示训练集中的项目总数。
因为权重反映了用户i相对于其他用户的相对重要性,所以需要将用户i的权重归一化,归一化公式如式(22)所示:
对于群组成员的可靠性,则根据每个成员的推荐准确率来设置。如果一个群组成员的推荐准确率非常低,那么就认为他不可靠,反之,推荐准确率越高,则越可靠,任意用户i的推荐精确率rpi如式(23)所示:
其中,Qt表示用户i正确推荐项目的数量,Qu表示用户i正确推荐列表上的项目数。
然而,大多数情况下没有人能够完全代表一个群组,这意味着没有人是完全可靠的,用可靠性的阈值S来限定用户的可靠性,用户i的可靠性如式(24)所示:
用户i的权重与可靠性的混合权重如式(25)所示:
基于上述条件,偏好融合的过程如下,将完整的用户-项目评分预测矩阵RM×N={ri,j}转化为证据资料矩阵PN×M=RTM×N={pv,i}。
若一个群组中只有两个用户,则融合结果可表示为如式(26)~(28)所示。其中,pv,E(2)表示群组对于项目v的预测值。
若一个群组中有两个以上用户,则使用递归方法进行融合,根据式(29)~(31)计算融合社群对项目的预测值pv,E(i)。
经过上述步骤,最终得到群组对项目的预测值pv,E(i),然后按照预测值高低将项目进行推荐,预测值越高,用户越有可能满意。本文提出的FPMF-ER群组推荐方法框架如图1所示。

图1 FPMF-ER群组推荐方法框架Fig.1 FPMF-ER group recommendation method framework
2.2 算法复杂度
下面对提出的FPMF-ER算法计算复杂度进行分析。本文算法主要由概率矩阵分解和基于ER规则的偏好融合两个部分组成,故算法的主要计算部分是更新潜在特征矩阵和证据融合时的递归运算。对于更新潜在特征矩阵,矩阵会反复更新,直至收敛,这一过程几乎与王英博等人[21]定义的过程相似,由此可知概率矩阵分解的时间复杂度是O(kDMN),其中,k是收敛所需的迭代次数,用户和项目分别由M和N的对应行表示,D是潜在特征向量。由于本文在经典概率矩阵分解算法的基础上联合了用户关系信息,所以每次迭代都需要额外的计算步骤。因此,上述优化过程的总计算复杂度为O(k(DMN+LM2))。其中,L是用户潜在特征向量。对于ER规则,它在偏好融合过程中采用正交和算子进行证据组合,此部分的计算主要是递归运算,时间复杂度为O(K(logn)),其中K是递归次数。通过ER规则进行偏好融合,能够大大减小传统证据组合的计算量,有效避免了组合爆炸问题,而且当面对大规模数据集时,算法的优势更明显。
3.1 数据集简介
本文在实验中使用了Book-Crossing数据集,该数据集包含278 858个用户、271 379本图书和1 149 780条评论,评论信息不仅包括文本,还包括用户对图书的数字评分,数字评分从1~10。
但是,该数据集并不包含分组信息,本文借鉴文献[22]的方式对数据集重构、进行群组划分:如果用户ui和用户uj评价了相同的图书,则将用户ui和用户uj划分到以该图书建立的一个群组。通过群组划分,重构的数据集中的278 858名用户共形成18 619个群组,规模最大的群组有29个成员,规模最小的群组有3个成员。本文从重构的数据集中随机选择80%的数据作为训练集,20%的数据作为测试集,数据集群组信息如表1所示。

表1 数据集群组信息Table 1 Data set group information
3.2 评价指标
对于推荐效果的评估,本文采用均方根误差RMSE作为评估推荐质量好坏的指标,采用归一化折损累计增益nDCG作为衡量生成Top-n推荐列表准确率的指标,采用满意度指标GSM衡量用户的满意度,具体计算方式如下所示。
RMSE的计算如式(32)所示:
其中,N表示社群中参与预测的项目数目;
ri表示用户对项目i的实际评分;
ri′表示用户对项目i的预测评分。RMSE结果的值越小,表示推荐的准确度越高。
nDCG的计算如式(33)、式(34)所示:
其中,{i1,i2,…,ik}是项目的评分列表;
g表示社群,n表示推荐列表的前n个;
rg,ik表示社群对项目ik的真实评分。nDCG是DCG的真实值与DCG的最大值的比值,DCG的最大值即推荐列表的最佳DCG值,nDCG的数值越大,表示推荐的准确度越高。
GSM的计算如式(35)所示:
其中,Nir表示推荐项目的个数,N表示社群中参与预测的项目数目,Ir表示推荐的项目。另外,为了提高实验的准确性和效率,需设置一个用户的满意度阈值,根据文献[23],满意度阈值过低,可能导致社群推荐整体准确性产生偏差,阈值设定过高,则不能真实地反映推荐项目与用户偏好情况。由于本文采用数据集评分为1~10,故将满意度阈值设置为7,即评分大于或等于7的成员对推荐的结果表示满意,故Isu表示7分以上的项目。
3.3 实验设计与结果分析
3.3.1 参数λU、λV和λF的选择
本文在联合用户关系的概率矩阵分解中有3个参数分别是λU、λV和λF,其中,λU和λV可以起到正则化系数的作用,相较于λF,λU和λV的取值较小,通常在0.001到0.01之间。为了探究上述参数对推荐效果的影响以及最优值,采用RMSE作为评价指标进行实验,在其他参数不变的情况下,参数λU和λV对推荐效果的影响如图2所示,λF对推荐效果的影响如图3所示。

图2 参数λU和λV对推荐效果的影响Fig.2 Parameters λU and λV on recommendation effect

图3 参数λF对推荐效果的影响Fig.3 Parameter λF on recommendation effect
从实验结果可以看出,当参数λU取值为0.002,λV取值为0.004时,RMSE值最小,此时推荐质量最高,故在后续实验中将参数λU的值设置为0.002,将λV的值设置为0.004。对于参数λF,当λF取0时,RMSE值最高,说明推荐的质量最差,此时FPMF将退化为经典PMF算法,而随着λF逐渐增大,RMSE值逐渐下降,推荐质量有所提高,当λF取值为8时,此时RMSE值最小,此时推荐效果最佳,故在后续实验中,将λF取值为8。
3.3.2 可靠性阈值实验
对于基于ER规则的偏好融合方法,用户的可靠性是一组相互没有影响的绝对值。它表示每个成员的可靠程度。虽然可靠性等于1代表“完全可靠”,但是几乎没有人能够完全能够代表一个群组,为了减弱这种影响,采用可靠度阈值S来约束群组内可靠性最高的成员。由于用户可靠性的取值范围是[0,1],且阈值设置不能太低,于是选择在[0.5,0.9]之间进行实验,探究最佳的可靠性阈值以及可靠性阈值对算法精度的影响,实验结果如图4所示。
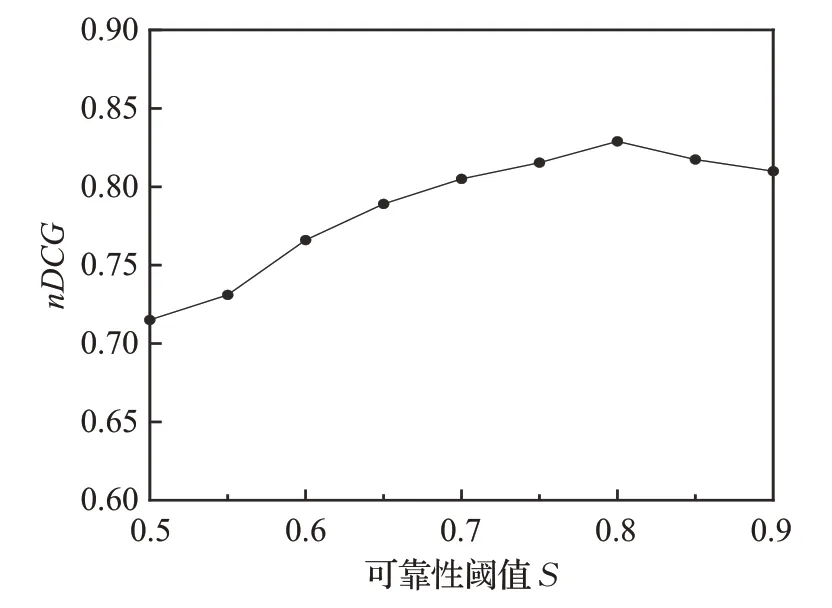
图4 可靠性阈值S对算法精度的影响Fig.4 Influence of reliability threshold S on algorithm accuracy
从实验结果可以看出,随着可靠性阈值的增大,算法精度的变化趋势是先增后降,当可靠性阈值取0.8时,nDCG达到峰值82.9%,此时算法精度最高,取得最佳性能,故在后续实验中,将可靠性阈值S设置为0.8。
3.3.3 潜在特征矩阵维度分析
潜在特征矩阵的维度会影响群推荐性能以及所提出模型的训练时间。在本小节中,分析不同维度对模型性能影响,实验测试在潜在特征矩阵维度d取不同值时,FPMF-ER模型的性能。设定潜在特征矩阵维度d的取值范围为10到100,选择nDCG作为评价指标,在Book-Crossing数据集上进行实验,实验结果如图5所示。

图5 不同潜在特征矩阵维度下的模型性能对比Fig.5 Comparison of model performance in different dimensions of potential feature matrix
从实验结果可以看出,随着潜在特征矩阵的维度d的逐渐增加,nDCG指标逐渐升高,说明FPMF-ER模型的性能有所提升。当潜在特征矩阵维度d达到80时达到饱和,模型的性能不再随着潜在特征矩阵维度d的增加而提升。
3.3.4 优化算法分析
本文在优化过程中使用了随机梯度下降(SGD)技术,为了探究不同优化算法对性能的影响,在本小节中选取了SGD、Momentum、RMSprop和Adam进行实验,实验结果如图6所示。从实验结果可以看出,相比与其他优化器,Momentum的效果较差,本文认为主要原因是Momentum积累之前的动量来代替真正的梯度,在训练初期时对训练速度虽有提升,但是比较难学习一个较好的学习率,导致较差的优化效果。RMSprop可以较好地修正收敛幅度,使各维度的摆动都较小,但是在应对稀疏矩阵时优化效果不佳,并且依然依赖一个不稳定的全局学习率。Adam能够动态调节每个参数的学习率,但是有可能会陷入局部最小值,最终会一直在最小值附近波动,并且面对大规模数据集时达不到较好的收敛效果。综合来看,对于本文来说SGD是效果最好的优化算法,它的每一步更新的计算时间不依赖于训练样本数目的多寡,对于大规模数据集或较为稀疏的数据集,SGD会在处理整个训练集之前就收敛到最终测试机误差的某个容错范围内,收敛速度和收敛程度均有较好的效果。

图6 不同优化算法的实验结果Fig.6 Experiment result of different optimization algorithms
3.3.5 算法复杂度比较分析
对于算法的时间复杂度方面,将本文算法与先进的群组推荐方法GROD和WBF进行对比分析。WBF方法首先将加权方案引入到评分矩阵中,然后将用户的偏好合并,并以一个虚拟用户来表示以构建群组偏好模型,最后通过矩阵分解算法获取群组推荐结果[24]。GROD方法通过在群组成员之间达成共识来考虑群组推荐中群组成员之间的关系,它的具体实现如下:首先使用SVD获得缺失的个人评分,然后使用获得的评分获得个人推荐并且获得群组用户之间的相似性矩阵,该相似矩阵用于在群组成员之间达成共识,最后使用意见动力学模型过滤与群组最相关的项目以产生推荐[25]。对于WBF方法,t1为迭代次数,K代表潜在因子矩阵大小,Ig是群组中至少一个用户评分的项目数,它的时间复杂度为O(t1(K2,Ig,K3))。对于GROD方法,t2表示迭代次数,k代表潜在因素矩阵的大小,I表示项目数量,Rg表示群组成员的最高评分量,该方法的计算复杂度为O(t2(gIk,g2Rg,g3))。分析可知WBF和GROD与本文算法在运行时间性能上的差异主要取决于迭代的运算复杂度与群组规模大小,WBF和GROD随着群组规模的增大效果降低较快,且迭代次数越高,时间复杂度越高,相较于WBF和GROD,FPMF-ER的时间复杂度更低,并且在大规模模数据集的实际应用中更为合适,具有较大的优势,时间复杂度比较如表2所示。

表2 算法复杂度比较Table 2 Comparison of algorithm complexity
3.3.6 准确度结果分析
本文使用4个对比方法,分别是PR-VU-GA-GR、LFM-AGRT、GRS-IT和LDA-GRS。
(1)PR-VU-GA-GR:采用推荐融合方法,单个用户偏好的拟合使用矩阵分解技术,偏好融合阶段使用一种基于虚拟用户的权重融合策略进行推荐[26]。
(2)LFM-AGRT:采用LFM隐语义模型对用户数据进行矩阵分解,通过将分解矩阵再次相乘获得用户对未评分项目的评分数据,然后采用加权混合融合策略对群组偏好进行融合[27]。
(3)GRS-IT:引入领导者影响的方法,结合皮尔逊相关性与一种隐式信任度计算找出组内领导者并获取领导者与成员、成员彼此之间的影响权重,然后采用均值策略对群组偏好进行融合[28]。
(4)LDA-GRS:采用模型融合方法,将组用户的偏好转化为整个群组的偏好,综合考虑群组用户的偏好以及信任关系构建了群组模型,基于此模型生成推荐列表[29]。
为了评估本文所提出方法在推荐结果准确度方面的整体表现,选取最优参数,使用RMSE和nDCG作为评价指标,在重构数据集上进行实验,分别比较群组规模在5、10、15、20、25时推荐结果的准确度。并且为了保证实验结果的公平性,实验进行5次测试再取平均值作为最终结果,选取RMSE作为评价指标的对比实验结果如图7所示,选取nDCG作为评价指标的对比实验结果如图8所示。

图7 推荐准确度的RMSE对比图Fig.7 RMSE comparison chart of recommended accuracy

图8 推荐准确度的nDCG对比图Fig.8 nDCG comparison chart of recommended accuracy
由图7和图8的实验结果可以看出,五种方法在群组规模扩大的过程中RMSE值均逐渐升高,nDCG值均逐渐降低,这说明随着群组规模扩大,推荐结果准确度有所降低。
其中,GRS-IT方法整体表现较差,原因在于该方法在偏好融合的过程中采用了传统融合策略中的均值策略,这种做法只是简单地将群组成员的评分取平均值,在融合过程中可能会丢失掉大量的有价值的信息,因此推荐结果并不可靠;
LDA-GRS方法采用的偏好模型融合方法在面临群组规模扩大的情况时,构建偏好模型的能力下降,导致推荐准确度下降,并且该方法未考虑群组中不同用户的权重应该不同,因此该方法在推荐结果准确度方面表现一般;
PR-VU-GA-GR和LFM-AGRT方法整体表现接近,且均优于前两种对比方法,原因在于在获取个人预测评分时,都采用了矩阵分解方法,预测单个用户的偏好拟合结果能力更强,因此推荐结果也更加准确,但是这两种方法在偏好融合时都同样设置了固定权重,随着规模的扩大成员关系会减弱,推荐准确度随着规模的扩大而降低;
FPMF-ER方法整体表现最优,原因在于该方法在单个用户偏好拟合阶段采用联合用户关系信息对概率矩阵分解进行改进,相比其他四种方法能够得到更加准确的个人预测结果,而且在偏好融合的过程中引入ER规则,为群组中不同用户设置有不同的权重和可靠性,随着群组规模的扩大仍然能够保持较高的准确度,避免了有价值信息丢失的问题,保证了用户偏好的准确融合,因此推荐结果的准确度更高。
3.3.7 用户满意度结果分析
用户对于推荐结果的满意度是评估的主要部分,因为群组推荐的目标是向群组推荐合适的项目,以最大限度地提高组成员的满意度,用户满意度实验将FPMF-ER与PR-VU-GA-GR、LFM-AGRT、GRS-IT和LDA-GRS进行比较,采用GSM作为评价指标,分别重复进行5次实验再将实验结果取平均值作为最终结果,并分别比较群组规模在5、10、15、20、25时群组成员的满意度,实验结果如图7所示。
由图9的实验结果可以看出,随着群组规模的逐渐扩大,各个方法的用户满意度均逐渐降低,FPMF-ER在规模为5、10、15、20、25时的GSM值分别为82.71%、79.54%、76.31%、74.22%、72.21%,且均高于其他四种方法的GSM值,原因在于FPMF-ER在偏好融合过程中能够为不同用户分配不同的权重和可靠性,识别出每个组成员的不同重要程度再进行偏好融合,能够更加真实地反映社会群体偏好选择过程,故而组成员的满意度较高。另外,五种方法的最高GMS值均是在群组规模为5时,分别为82.71%、79.27%、78.35%、74.32%、69.12%,且随着规模的扩大GSM逐渐降低。实验结果可以看出五种群组推荐方法的用户满意度排序为:FPMF-ER>LFMAGRT>PR-VU-GA-GR>LDA-GRS>GRS-IT。

图9 用户满意度对比图(GSM)Fig.9 Comparison of user satisfaction(GSM)
本文提出了一种新的融合概率矩阵分解与ER规则的群组推荐方法,在单个用户偏好拟合阶段,采用联合用户关系的概率矩阵分解方法获取个人预测评分,能够准确而稳定地预测单个用户的偏好。在群组用户的偏好融合阶段采用一种基于ER规则的偏好融合方法,该方法能够根据不同用户的权重和可靠性,准确识别出用户的重要性,使融合过程更加准确合理。在真实数据集Book-Crossing进行了实验,以验证本文所提出方法的有效性。结果表明,相对于其他方法,本文所提出的FPMF-ER方法在推荐结果的准确性和用户满意度方面有较大的提升,具有较高的推荐质量。
本文工作的局限性在于所使用的数据集针对性较强,不能保证算法的普适性,下一步的研究方向是选取其他数据集和评价指标进行更有力的验证。另外,在未来的研究中,仍有许多其他有效的偏好融合方法有待发现和改进,接下来将继续从偏好融合方面进行研究,提出更高效的偏好融合方法,不断提高群组推荐的效果。
猜你喜欢群组矩阵融合村企党建联建融合共赢今日农业(2021年19期)2022-01-12融合菜中老年保健(2021年11期)2021-08-22从创新出发,与高考数列相遇、融合中学生数理化(高中版.高考数学)(2021年1期)2021-03-19《融合》现代出版(2020年3期)2020-06-20初等行变换与初等列变换并用求逆矩阵中央民族大学学报(自然科学版)(2016年3期)2016-06-27基于统计模型的空间群组目标空间位置计算研究山西大同大学学报(自然科学版)(2016年6期)2016-01-30矩阵南都周刊(2015年4期)2015-09-10矩阵南都周刊(2015年3期)2015-09-10矩阵南都周刊(2015年1期)2015-09-10群组聊天业务在IMS客户端的设计与实现计算机工程与设计(2011年7期)2011-09-07