蒋佩伶,王志松,蒋 越,刘 浩
(1.江西理工大学电气工程与自动化学院,江西 赣州 341000;
2.江西理工大学应急管理与安全工程学院,江西 赣州 341000;
3.江西理工大学信息工程学院,江西 赣州 341000)
通过对我国离子型重稀土储量进行统计分析可知,赣州市重稀土储量在国内同类型矿山储量排行中位居第一。为了推动赣州地区经济持续发展,大量企业对赣州市稀土矿产资源进行了大规模开采,直接导致矿区的地质环境越来越差。选用池浸、堆浸和原地浸矿的工艺开采方式使矿区土壤越来越松散,在降雨等恶劣天气影响下,极其容易滑坡,使当地生产发展和居民生活的安全难以得到保障。近几年,国家出台相关法规对耕地进行保护,许多矿区为减少占地面积,不得不在原来的尾矿上进行二次堆积,长时间开采所形成的尾矿废渣堆积也越来越高,据统计,赣州市超过200 m的尾矿达30多处[1]。
赣州市的尾矿主要位于山区,地势复杂,矿区分布分散,导致监测成本高、难度大,不能集中统一监测。由于稀土利润巨大导致难以监管,许多私企在偏僻地段的开采屡禁不止。赣州市稀土开采的规模持续扩大,直接导致矿山裸露地表区的土壤侵蚀越来越严重。与一般土质边坡的性质相比,尾矿的废渣堆积存在结构无序、弱胶结或无胶结的性质,规律和破坏模式差异较大[2-3],给离子型稀土矿环境综合治理工作埋下了重大的安全隐患。赣南地区雨水丰沛,特别是在每年的梅雨季节,受持续强降雨等极端天气影响,雨水会深层次渗入边坡,极易产生局部垮塌甚至大规模的滑坡灾害[4-6]。如图1所示为赣州市某尾矿滑坡实拍,如果类似的尾矿边坡处于上游地区,滑坡灾害所造成的损失还将成倍增加。

图1 赣州市某尾矿堆积实拍Fig.1 A real shot of a tailings accumulation in Ganzhou City
边坡的滑落破坏除了降雨以外还由很多其他因素导致,如边坡的坡角大小、干滩比、活动荷载、内摩擦角、裂隙大小和深度等,对于这些因素前人进行了很多研究,也进行过相关数值模拟。但对于在降雨作用下单独分析裂隙这一因素的数值模拟还比较少,加之国产数值模拟软件近几年处于推广过程中,也缺少相关的研究分析。因此,本文以60°边坡作为高陡边坡中的一个特例,对其在降雨条件下的边坡含水率和位移的演化规律进行相关研究。
1.1 MatDEM简介
离散元法(DEM)基于分子动力学纳米技术,最早主要应用于物理学和流体动力学。该方法自从Cundall引入研究颗粒集合的力学行为以来开始受到关注。经过几十年的发展证明,离散元已经成为一种广泛应用的数值计算方法,特别是在岩土力学研究中,其整体力学性质的数值模拟可以与物理实验进行对比分析。本文采用国产自主研发的离散元软件(MatDEM)进行数值模拟。MatDEM基于矩阵离散元法,在单元数量和运行速度方面与同类型软件相比有明显的优势,极大地方便了数值模拟。
1.2 降雨入渗与水分传输过程
土颗粒、孔隙和孔隙水构成MatDEM中一个离散元单元,因此每个单元可以设置和传输一定量水分,并通过把有限差分思想运用到数值模拟中,计算单元水分迁移量,MatDEM就可以实现对水分场的模拟[7-8]。同时,考虑水分场对土体抗拉强度等力学性质的影响,可以最终得到水分场和位移场在一定时间内的演化规律。
模型中每个单元颗粒的含水量代表颗粒大小区域内的平均含水量。雨水落到边坡表面再向下传播,每个时间步单元增长含水率计算见式(1)。

(1)
式中:ω为颗粒每次计算时的含水率;
mw为本次迭代增加的含水量;
mw0为本次迭代计算时的初始含水量;
ms为固体颗粒的重量。
根据达西定律描述土体渗流场内水头的分布规律,水分由高水头向低水头迁移,进而实现降雨入渗的过程,计算见式(2)。

(2)
式中:Q为渗流的流量;
H1-H2为水头损失;
A为流过颗粒的断面积;
L为渗流通过的长度;
k为渗透系数,表示孔隙在透水方面的物理性质。只有当总水头差Δh>0时,水才会发生从总水头高的点向低的点流动。降雨入渗过程是非饱和土体变为饱和的过程。因此,本文将颗粒间总水头简化为位置水头。以图2中白色基本单元为例,其会向周围相对其水头较低单元传递水分。根据达西定律,当白色颗粒会传递水分给下方三个黑色颗粒时,若两者间水力梯度值大则水分传递量越大。因此假定在一个计算步内,相邻两单元水分传递量与两者含水量差值以及水力梯度值有关,白色单元向传递给1号单元的含水量计算见式(3)。

(3)
式中:i01、i02以及i03分别为白色颗粒与三个黑色量之间的水力梯度值;
ω0、ω1为白色颗粒与1号单元的含水量。1号单元在被传递dM01后,白色单元会减少相应的含水量,实现了水分运输守恒,通过以上理论和方法继而实现降雨水分场演化。

图2 水分传递示意图Fig.2 Schematic diagram of moisture transfer
1.3 离散单元的材料
在离散元建模中,建模重点和难点之一就是确定模型中每个单元力学参数。因此,MatDEM中存在一个转换公式使堆积模型的宏观力学性质和微观力学参数相互转换,使离散元堆积材料具有特定弹性模量和强度性质,并用于边坡岩土不同地层之中,通过使用训练后的材料就可以实现相同类型模型的建模自动化[9]。如果模拟模型是线弹性模型,微观力学参数就可以通过五个宏观力学参数性质计算得到,分别是杨氏模量、泊松比、抗压强度、抗拉强度和内摩擦系数。该模型通过不断的材料数值测试和自动调整,得到所需要的五个宏观力学参数。为了减少模型的力学性质与设定值之间的差异,函数还会自动将设定值乘以相关系数再代入相关公式,本文对尾矿的不同材料设置详见表1。
1) 随机堆积模型。废弃稀土尾矿堆积的边坡土壤主要表现为一种各向异性、结构无序、弱胶结或无胶结的特殊地质体。因此,模型通过在堆积模型时设置分散系数来实现这一现象[10],在模型箱内生成平均半径为0.03 m的随机单元并压实这些单元,来替代实际中岩土颗粒的沉积过程。如图3所示,建立一个高为8.5 m、宽为12 m的长方形初始堆积模型。

表1 尾矿的材料Table 1 Material of tailings

图3 初始堆积模型Fig.3 Initial stacked model plot
2) MatDEM分层和赋予材料。MatDEM可以利用导入的坐标点文件生成不同划分地层,只要确定地层边界坐标点就可以对任何复杂二维模型进行建模,极大地降低了使用者的建模难度。
编写边坡模型代码导入MatDEM后,生成一个坡顶长为2 m、坡底长为4.73 m的尾矿堆积体,然后对完成分层的模型进行裂隙设置。由于裂隙生成比较复杂,所以模型中使用软弱层来替代裂隙的影响效果。又因为单元之间孔隙的存在,边坡裂隙含水率高于其他边坡内部区域含水率。具体设置为边坡裂隙含水率为常数0.3,非裂隙区域含水率为常数0.1。
3) 设置降雨。降雨为发生滑坡的重要原因之一[11-13]。在MatDEM代码中,选取边坡最外层为雨水层,并设置其含水率不变且为最高,具体设置雨水层的含水率为常数0.9,只要雨水层的含水率不发生变化,就可以表示降雨在持续进行。
4) 建立观测区。为了便于分析,建立四个观测区,每个观测区中有300多个单元和两组数据(图4)。
观测区域1取z值为5.75~6.25 m,且x值为1.75~2.25 m的所有单元颗粒,观测区域2取z值为3.75~4.25 m,且x值为1.75~2.25 m的所有单元颗粒,观测区域3取z值为3.75~4.25 m,且x值为3.75~4.25 m的所有单元颗粒,观测区域4取z值为1.75~2.25 m,且x值为3.75~4.25 m的所有单元颗粒。观测区1和观测区2的高差与观测区3和观测区4的高差相同,均为2 m。此外,观测区2和观测区3的水平距离也为2 m,这一设置除了方便进行数据定量分析外,还可以让一个观测区内的单元同时拥有裂隙区单元和非裂隙区单元。
本文完成了强降雨作用下边坡从失稳、单元颗粒连接断裂到整体滑移的全过程模拟,该过程共历时约36 s,计算机模拟耗时约5 h,共生成12个MatDEM文件和8个供分析的数据表,主要数据为含水率、位移变化、配位数以及单元速度。通过对数据提取、分类、筛选、分析, 得出位移场、水分场和裂隙演变规律。
3.1 水分场演变规律
为了对持续降雨环境进行模拟,设定最顶层颗粒单元的含水率为常数0.9。模拟结果显示,在强降雨条件下,水分持续入渗,并导致边坡滑移。图5为坡体内的含水率时程分布图。
由图5可知,在3 s、15 s、24 s、27 s时刻,分别入渗到坡体内约为1 m、2.5 m、3 m、4 m位置。坡体内含裂隙区域含水率的变化速率明显较高,在这几个时刻,分别入渗到距离破顶面约为1 m、3.5 m、4.5 m、6 m位置,其渗流速率约为非裂隙区域2倍左右。

图4 边坡模型示意图Fig.4 Schematic diagram of slope model

图5 含水率的时程分布图Fig.5 Time-history distribution of moisture content
图6展示了单元含水率变化情况。由图6可知,A观测点、B观测点、C观测点、D观测点依次为观测区1、观测区2、观测区3和观测区4的非裂隙区单元观测点;
E观测点、F观测点、G观测点、H观测点依次为观测区1、观测区2、观测区3和观测区4的裂隙区单元观测点。随着时间的推移,四个观测区所有单元的含水率均会逐渐增加。在图6(a)中,非裂隙单元含水率从0 s时就开始变化。除了A观测点与D观测点的含水率变化曲线在6.1 s出现增速变化外,四个观测区中的单元含水率曲线并未发生较大的增速变化。6.1 s之后,四个观测点的含水率曲线并未发生较大的波动,从高到低依次为ωC、ωA、ωD、ωB。在图6(b)中,裂隙区内单元含水率变化出现在6.1 s之后。在10.7 s之前,单元含水率变化由高到低排列分别为ωG、ωE、ωH、ωF,其中,ωH和ωF含水率相等。10.7 s之后,裂隙区单元含水率由高到低排列分别为ωE、ωG、ωF、ωH。其中,F观测点的含水率变化从15 s开始逐渐增加,H观测点的含水率变化在21.1 s之后开始增加。
为了研究三个观测区的单元含水率变化,分别对观测区中的八个观测点的单元含水率差值进行分析。如图7(a)所示,在非裂隙单元中,ωC-ωD差值曲线始终高于ωA-ωB差值曲线,且分别在15 s时达到含水率差值峰值,出现这类现象的原因主要是C观测点处在坡底靠近边坡面,而A观测点与B观测点的位置靠近裂隙,水分传输较快,含水率差值反而较小。与图5所示15 s时含水率变化曲线进行对比分析可以发现,在15 s时,水分一直沿着裂隙带迁移,水分的传导层达到观测区1附近,湿润锋达到观测区2附近,而在观测区4没有水分尚未入渗。在图7(b)中,又对裂隙单元的含水率差值进行了对比,可以发现,在11 s前,ωG-ωH差值曲线高于ωE-ωF差值曲线。出现这一现象的主要原因是G观测点的位置要比E观测点更靠近坡面,水分迁移更快。
在10~18 s之间,两条差值曲线高低发生改变,水分开始沿着裂隙带向下加速迁至E观测点, 所以ωE-ωF差值曲线高于ωG-ωH差值曲线,ωE-ωF差值曲线在15 s出现最高点,最高点的含水率差值为常数0.375。在18 s时,出现两条曲线的第二个交点。18 s之后,ωG-ωH差值曲线高于ωE-ωF差值曲线,并且ωG-ωH差值曲线在26 s达到最高点,其含水率差值约为常数0.31。出现第二个交点的原因主要是:在18 s时,裂隙带上层的单元滑落,G观测点与边坡表面的水分传输距离缩短。整体来看,随着时间增加,四个观测区单元含水率都逐渐趋于饱和,增速也明显变缓,在分别达到含水率差值峰值之后,差值曲线都出现了下降的趋势,意味着四个观测区单元含水率将逐渐趋于饱和。
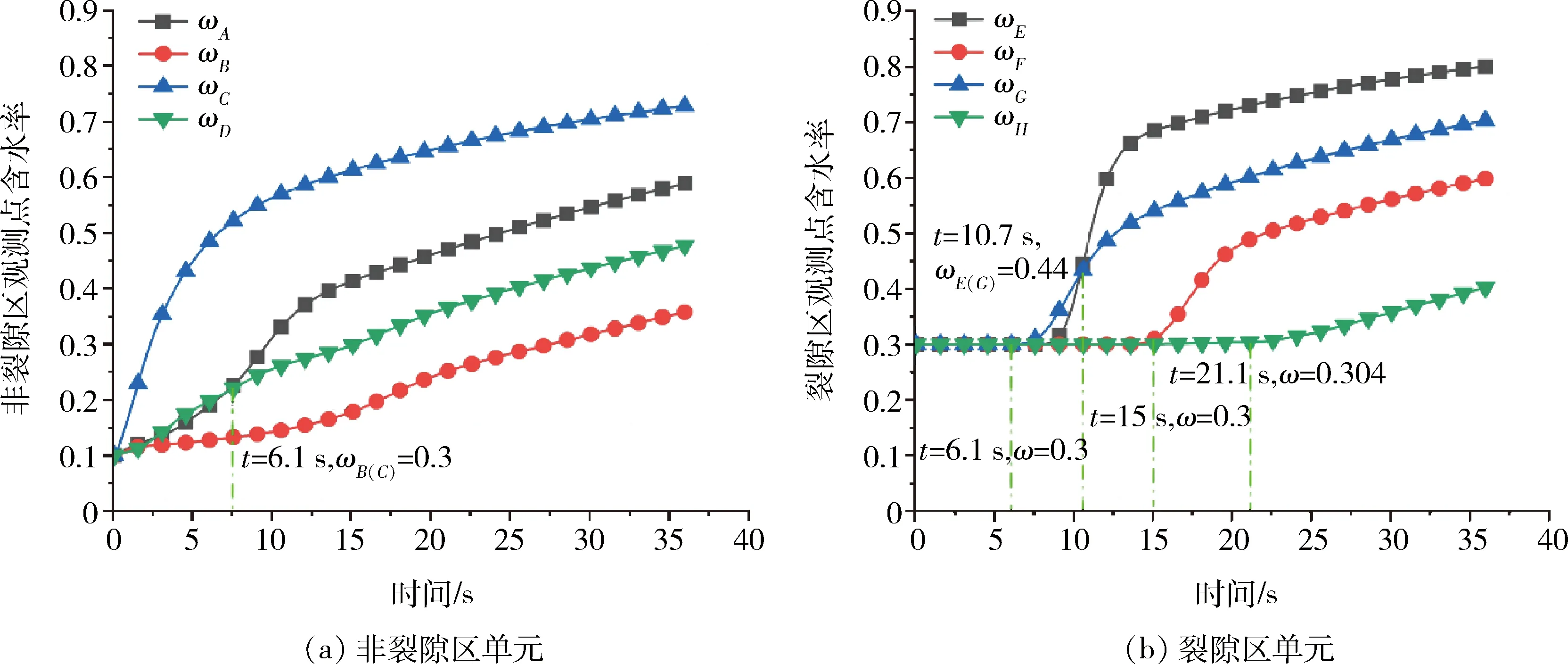
图6 单元含水率变化曲线Fig.6 Change curves of unit water content

图7 含水率差值变化曲线Fig.7 Change curves of water content difference
单独取观测区1、观测区2和观测区3中的六个观测点,进行单元水分横向迁移与纵向迁移的快慢分析,并探究裂隙是否对水分迁移有一定的作用。因为前面已经设置三个观测区的直线距离为2 m,可以对三个观测区进行相同水分运距和时间、不同方向的含水率差值对比分析,如图8所示。由图8可知,15 s附近三个观测区的含水率差值同时达到峰值。并且从图8(a)中还可以看出,ωA-ωB差值曲线始终高于ωC-ωB差值曲线,说明纵向水力梯度要大于横向水力梯度。相比于非裂隙区单元而言,在图8(b)中,裂隙区单元含水率差值却在10.1 s出现一个交点。在10.1 s之前,裂隙区单元与非裂隙区单元含水率差值变化一样,但在10.1 s之后,裂隙对雨水迁移开始影响含水率的差值变化,ωG-ωF差值曲线高于ωE-ωH差值曲线,不同方向的水力梯度大小变为横向水力梯度大于的纵向水力梯度。这一变化与非裂隙区有明显差别,由此可以得出裂隙对水力梯度的大小有一定的影响。

图8 不同方向含水率差值变化曲线Fig.8 Change curves of water content difference in different directions
3.2 位移演变规律
3.2.1 观测区滑落位移分析
在高降雨强度条件下,边坡的滑落破坏极其容易产生[14-16]。与整体破坏滑坡有所不同,因降雨入渗裂隙导致孔隙水压增加的非整体破坏滑坡,往往是从裂隙引发的局部滑坡,并在雨水和自重作用下滑落至边坡底部[17-18]。由图9可知,当降雨入渗9 s后,分别在距离坡底1 m、2.5 m、6.5 m的位置出现了小规模的下沉破坏。当降雨入渗18 s后,边坡沿着裂隙出现分层滑坡,水分使裂隙区域单元连接断开,连接断开的单元颗粒在重力和孔隙水压的双重作用下产生长约5 m的断裂带。随着降雨继续进行至27 s,破坏范围逐渐扩大,滑体部分的颗粒含水率基本达到饱和,滑体最底端由2 m的高度冲击到地面,滑体最上端的高度由7 m降至为4 m。当降雨入渗36 s后,滑落部分完全下降至底层地面,也代表着尾矿边坡滑落完全结束。
3.2.2 移动滑体量分析
降雨入渗使排土场体内含水率饱和区域迅速增加,并不断下移扩散,排土体自重增大[19]。
在MatDEM中,筛选X轴方向移动速度大于0的单元,每0.1 s计算其面积之和作为移动滑体量,如图10所示。由图10可知,在整个边坡失稳过程中,受降雨影响的移动滑体量一直围绕在0 s后均线12.7 m2附近上下变化,并未发生太大的变化。在0 s时,边坡未受到雨水侵蚀,单元也没有任何移动,在1~6 s和12~22.5 s之间,受单元自身摩擦力的影响,产生两个移动滑体量波动范围较大的区域,特别是在16.5 s附近,移动滑体量出现一个最大振幅,由8 m2增加到17.5 m2。在21 s之后,移动滑体量的波动范围趋于稳定,单元移动滑体量仍在均线12.7 m2附近。

图9 位移变化图Fig.9 Diagram of displacement change

图10 移动滑体量Fig.10 Move slider amount
3.3 裂隙的演变规律
3.3.1 单元连接演变规律
裂隙作为优势入渗通道,使得雨水能快速沿着裂隙渗入到坡体内部。同时,裂隙内水体入渗属于有压入渗[20],与边坡表面的入渗相比,裂隙入渗的速度更快,对边坡的破坏作用也较大[21-23]。在MatDEM中,单元之间连接如图11所示。其中,边坡内部的非空白区域表示单元连接,增加的空白区域表示单元连接断开。随着水分开始入渗边坡内部,裂隙单元连接逐渐断开,并开始出现滑坡。与边坡移动过程图不同,降雨对裂隙单元间连接的破坏并不是36 s后才结束。由图11(d)可知,单元之间连接在21 s前就完全断开,并且单元连接沿着裂隙向上和向下都有断开。以最内侧裂隙带为例进行分析:在6 s时,上方空白区域长约为1.5 m,下方空白区域长也约为1.5 m。但在18 s时,上方空白区域长约为5 m,下方空白区域长约为2 m,说明单元连接向下断开的速度比向上断开的速度更快。

图11 单元连接变化Fig.11 Changes of unit connection
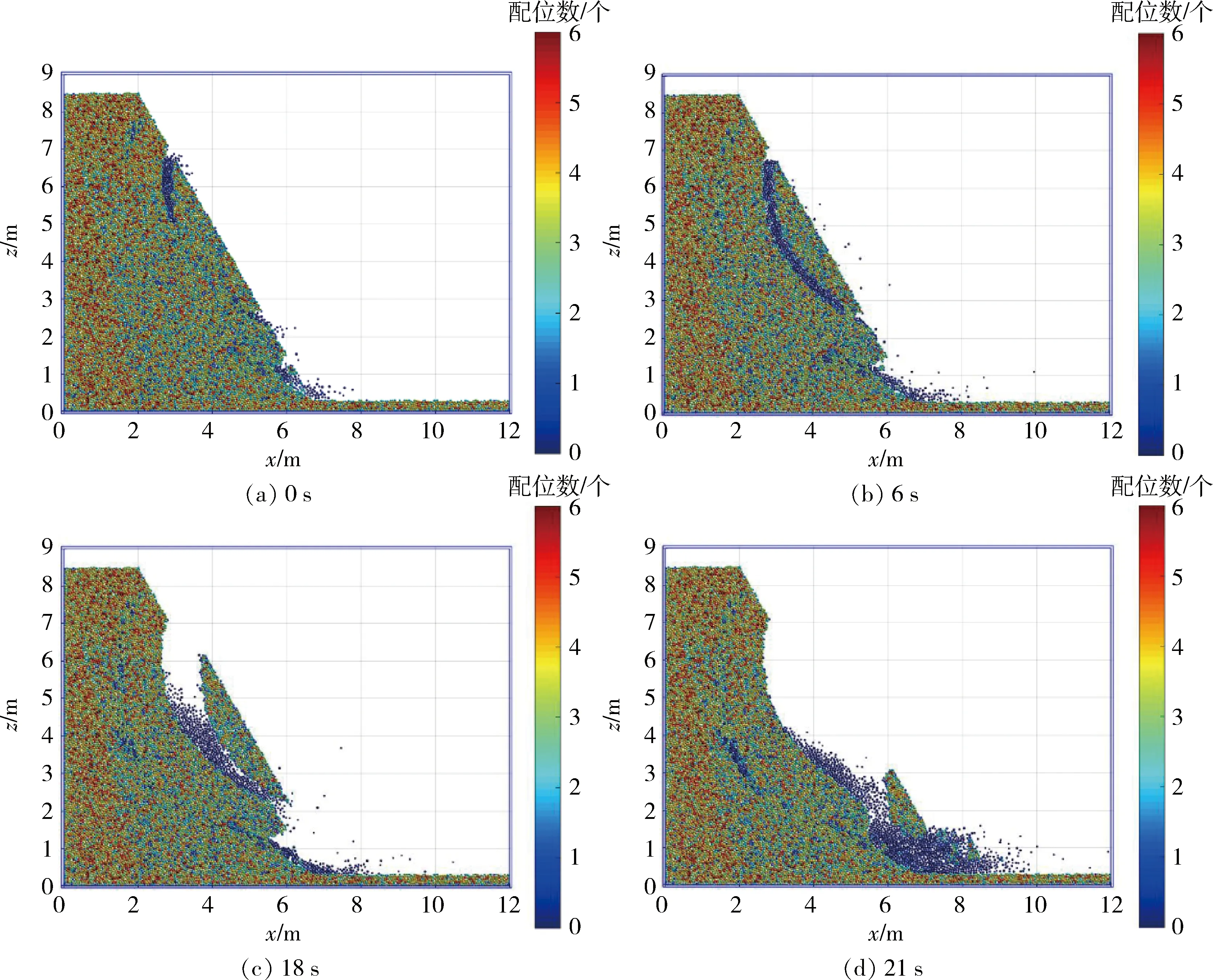
图12 边坡配位数过程图Fig.12 Process map of slope coordination number
3.3.2 配位数演变规律
在MatDEM中,一个单元颗粒周围连接了许多颗粒,而配位数就是某一单元颗粒周围颗粒的数量之和,它反映单元密实程度[24],如图12所示为单元配位数变化过程。配位数主要受单元连接断开影响而发生变化,如果单元连接断开,则单元配位数会下降。在本文模型中,只要裂隙单元含水率超过常数0.5,则裂隙单元连接就会断开,单元配位数也同时会减小。因此,配位数的变化还间接反映降雨对单元密实程度的影响。除此之外,非裂隙单元在受到外界力量或单元自身重力时,也会造成配位数发生改变。由图12可知,在18 s之前,配位数主要受降雨的影响在裂隙处变化。通过配位数的变化,裂隙单元之间的连接力下降,裂隙和边坡堆积岩层相互之间的作用力也同时减小,使边坡更容易滑落。在18 s之后,配位数的变化主要受自身重力的冲击影响而增加,滑体向下冲击,使部分滑体前端部分的配位数下降至2个以下。
由于无法预先确定滑体的位置和滑体量,因此无法求得在滑落过程中的配位数,但是可以通过筛选配位数小于2个的单元,求得单元面积和来表示配位数的改变量,从而反映配位数量的变化趋势。如图13所示,0~36 s之间的配位数面积和一直在增加,反映出边坡密实程度一直减小。0~9 s之间,受降雨影响,小于2个的配位数量的单元面积和增长比较快,说明单元的密实程度变化较快。在滑落中间阶段,即21~27 s,受滑体冲击地面的影响,配位数小于2个的单元面积和出现第二次快速增加,证实了在冲击力的影响下,单元的密实程度也会进一步减小。在27 s之后,滑体大部分落至地面,滑落基本结束,配位数量变化趋于稳定,说明单元密实程度最终趋于稳定。

图13 配位数变化趋势图Fig.13 Variation trend graph of coordination number
1) 降雨入渗到裂隙区域并导致裂隙的单元连接断开,边坡稳定性发生改变,裂隙处的配位数即密实程度下降,在持续降雨作用下,最终导致了滑坡的发生。
2) 0 s之后,受降雨影响的滑体移动总量并没发生太大改变,这说明降雨对滑体移动的量并没有太大影响。
3) 将模拟得到的水分迁移以及位移场变化规律与室内试验及前人研究结论相对比,可以比较清楚地观察降雨诱发滑坡的全过程,能够较为有效地进行降雨诱发滑坡模拟,为利用离散元法模拟降雨诱发滑坡过程提供了一个崭新的思路。
4) 赣州市尾矿边坡的预防和管理工作主要是以防止开采、标准化和风险发生时的早期警告为目的。特别是在赣州市的梅雨季节,降雨会持续相当一段时间。了解边坡不稳定性机制,特别是对于高陡边坡的数值模拟研究分析,有助于治理赣州市尾矿边坡的治理,减小滑坡发生的可能性。
猜你喜欢观测点配位差值[Zn(Hcpic)·(H2O)]n配位聚合物的结构与荧光性能四川轻化工大学学报(自然科学版)(2021年1期)2021-06-09扎龙湿地芦苇空气负离子浓度观测研究现代农村科技(2021年2期)2021-03-15差值法巧求刚体转动惯量高师理科学刊(2020年2期)2020-11-26洛阳市老城区西大街空间形态与热环境耦合关系实测研究绿色科技(2019年12期)2019-07-15德不配位 必有灾殃当代陕西(2019年6期)2019-04-17数值推理的扩展研究数理化解题研究(2018年10期)2018-04-02枳壳及其炮制品色差值与化学成分的相关性中成药(2017年6期)2017-06-13基于升降温全曲线的钢筋混凝土梁温度场分析山东建筑大学学报(2015年4期)2015-05-11基于区域最大值与平均值差值的动态背光调整安徽工业大学学报(自然科学版)(2014年4期)2014-07-11两个具stp三维拓扑构型的稀土配位聚合物{[Ln2(pda)3(H2O)2]·2H2O}n(Ln=Nd,La)无机化学学报(2014年4期)2014-02-28