冯宇豪, 陈得意, 曾磊, 王振宇, 贺月洁
(长江大学城市建设学院, 荆州 434023)
近年来,随着新型材料和复杂的结构形式逐渐应用到人行桥中,现代人行桥呈现出轻质、低阻尼、大跨度的特性,在行人荷载激励下易产生大幅振动,影响行人舒适性和安全性[1-2]。因此,振动舒适性成为人行桥设计中需要考虑的关键问题,其量化评估是研究难点。
结构振动水平在一定程度上反映了行人的舒适程度。评估人致人行桥振动舒适度,现有规范以及国内外学者大多采用结构某一代表值作为评价指标[3-4]。英国规范BS5400[5]明确规定:人行桥竖向振动自振频率大于5 Hz时,其人致振动舒适度一般能满足要求。谢伟平等[6]通过研究结构竖向基频与人致振动响应之间的关系,建议满足舒适度要求的竖向基频限值应大于3.3 Hz。曹雷等[7]基于智能手机展开网络振动测试和问卷调查,采用数据清洗原则和筛选,统计得到了不同影响因素所对应的振动限值。但实际情形中,即使人行桥动力特性不在规范所建议的限值范围内,也可能满足舒适度要求。因此,舒适度评估需要向更精细化的方向发展。Zivanovic等[8]考虑步行荷载的非周期性,从统计和概率论的角度建立了随机时域模型,并用概率的形式对单人过桥的振动舒适度进行评价。朱前坤等[9-10]建立了基于激励-传播-感知全路径的振动舒适度分析框架,并以超过特定加速度响应的累计概率对结构舒适性进行评价。评价指标非单一值而是概率值,但该类研究并未考虑人体主观感受与结构振动物理量之间的关系,由于人对振动的感受是人的生理和心理机能对振动的客观感知和主观判断的综合效应,其本身就具有不确定性,需建立能准确描述行人心理与结构振动之间关系的定量化模型。
针对人致振动舒适度定量计算模型,已有大量学者开展了研究。宋志刚[11]从心理物理学出发,通过建立隶属度函数将行人对振动的模糊感受进行量化,首次提出了烦恼率模型,并用烦恼率作为描述振动舒适性的量化指标。文献[12-13]结合烦恼率模型以及传统舒适度评价标准,提出了考虑结构竖向与侧向耦合振动的综合评价方法。陈彦江等[14]利用Hilbert-huang变换研究不同环境激励下的人行桥振动响应,引入能量嫡值对功率谱和能量分布的变化规律进行描述。王振宇等[15-16]建立4种考虑时-空多尺度的随机行走模型,分析对比了各模型下峰值加速度响应的变化规律。申选召等[17]基于随机步行荷载,经行大量时程分析得到结构最大均方根加速度累积概率分布,计算出结构反应的烦恼率期望值,进行舒适度评价。Chen等[18]引入人体抗力和振动效应及敏感度新概念,将行人承受振动能力进行量化,推导了敏感度的计算表达式。
以上研究皆是对人致振动舒适度量化评估的有益探究,在建立定量化模型方面做了大量贡献。然而,仍有较多问题有待解决:①衡量舒适度的指标多从结构方面展开,但结构振动响应并非等同于行人实际感受到的振动,建立能更准确描述行人振动感受的舒适度指标尤为重要;②人行桥振动往往是由随机人群荷载激励引起,行人步态参数的随机性导致了人行桥振动响应在某个域内呈现概率分布,因此采用单一工况对人行桥舒适度进行评价不具有说服力;③目前考虑行人主观感受模糊性的舒适度定量计算研究较少,隶属度函数的合理确定问题尚未解决。
针对以上问题,现对结构峰值加速度与行人实感响应之间的相关性进行研究,给出振动响应折减系数的定义以及取值;同时,联系行人在心理连续体上的区间划分是非等距的,基于Stevens幂函数定律的隶属度函数,对传统烦恼率模型进行了改进;最后,提出基于行人实感和烦恼率模型的人行桥振动舒适度评价方法,并对荆州市某人行天桥进行舒适度评估验证本文方法的合理性。
人致人行桥振动舒适度评估常采用结构产生的峰值加速度作为评价指标[19-20]。然而,在实际人行桥人致振动过程中,由于同一时间,不同行人因所处位置不同所感受到的振动响应不同,同一位置因时间不同感受的振动响应也不同。即同一工况下,各行人感受到的最大振动响应是不相同的。因此,将结构产生的峰值加速度作为评价各行人烦恼程度的指标显然是不合理的。而行人是评判人行桥舒适与否的唯一感知体,在评估振动舒适度时,有必要将行人实感的加速度峰值作为评价的参考依据。
1.1 随机人群模型
人群对人行桥的激励作用完全是随机过程,行人产生的激振力随步行参数的变化而变化。为研究行人实感最大响应和结构最大振动响应异同,采用Monte-Carlo法描述随机人群步行荷载进行时程分析,假设人行桥桥跨为L,宽度为B,行人i初始位置为(xi0,yi),考虑行人随机性的行走模型如图1所示。

图1 随机行走模型Fig.1 Random walk model
为准确反映行人各时刻在桥上的位移,采用基于步长叠加的行走模拟方法。根据文献[21]建立的行人步速与步频的关系为

(1)

(2)
式中:vij为行人i第j步的步速;fpij为行人i第j步的步频;tij为行人i走完第j步需要的时间;lij为行人i第j步的步长。
对于人致大跨人行桥振动分析,需要确定每个行人在桥上的空间位置,由行人在桥上的初始位置,利用式(1)和式(2)可计算行人i走完每一步的时间,根据时间t对有限段步长进行叠加可计算行人i在桥上具体的位移xij为

(3)
式(4)中:Ni为行人i走完全程需要的步数。
随机人群激励荷载为

(4)
式(4)中:fpi为第i个行人的步频;G为行人重量;αki为第i个人在第k阶步行荷载分量的动力因子;φki为第i个人在第k阶谐波的相位;t为时间。
行人步频fp、初始相位φ、自重G及所处结构位置(x,y)均为满足一定分布规律的随机变量,对以上变量进行了如下假设:①行人步频服从正态分布N(1.825,0.221);②行人初始相位角,假设行人起步属于完全随机步行,取初始相位服从区间[0,2Π]内的均匀分布;③行人体重与其他步行参数无关,其随机性对计算结果影响较小,为方便计算,行人体重G取为67 kg;④初始位置,行人在桥上的位置分布是等概率的,因此行人初始位置考虑为均匀分布U(0,L)。
1.2 振动响应分析与对比
在桥面等距划分11个点位,按上述参数所作假设生成100组随机荷载,通过时程响应分析提取每组工况的峰值加速度,同时,由式(3)计算出行人各时刻在桥上的位移,结合模型划分点位的时程响应,可提取各行人在过桥总时程内承受的最大加速度。各工况下行人承受最大振动响应分布以及结构峰值加速度分布如图2所示。
从图2可知,结构跨中峰值加速度和行人实感最大加速度在分布上差异明显,考虑行人实感的加速度较峰值加速度出现了在区间0~0.1 m/s2的分布,且整体分布相对靠近左侧,说明行人在实际过桥中感受到的振动响应是小于结构峰值振动响应的。
图3为结构峰值加速度与行人实感加速度累积概率分布。若规定人行桥加速度限值为0.3 m/s2,由对比结果可知,行人实感振动响应超过0.3 m/s2的累计概率为4%,而结构峰值加速度超过限值的累计概率为35%。显然,利用人行桥振动反应的代表值进行舒适度评价是不合适的,很大程度上低估了人行桥的振动舒适性;而考虑行人个体实感时程的差异性,采用各行人在实感时程内的最大加速度作为舒适度指标,能更精确的评估人行桥振动舒适度。

图2 加速度分布Fig.2 Distribution of acceleration

图3 累积概率分布对比Fig.3 Comparison of cumulative probability distribution
1.3 振动响应折减系数
利用行人实感时程量化振动舒适度的前提是获取每个行人的时程响应,但在实际应用中,实感时程无法通过实测得到,需要对结构总时程响应分析处理,其工作量大、效率低。针对上述问题,结合数值分析方法,通过统计计算可得到每组工况下行人实际感受的振动响应,从而建立起峰值加速度amax与行人实感最大加速度均值at之间的相关关系,如图4所示。

图4 峰值加速度-行人实感Fig.4 Peak acceleration-acceleration of pedestrian feeling
根据图4中的拟合对比结果可以看出,行人在行走过程中感受到的最大振动与结构峰值加速度存在较强的相关关系。由于该模式下振动响应近似服从正态分布,在中心区域较为集中,三条拟合曲线高度重合,其中线性拟合效果最好,拟合精度达到0.912 4。因此采用线性形式为
at=0.568amax+0.022 7
(5)
由式(5)分析可知,当峰值响应趋近0,行人实感响应均值会逐渐接近并超过峰值加速度;而当峰值响应逐渐增大,两者间间距先不断变大后呈比例关系。这是由于式(4)是在本文模型基础上建立的,其峰值加速度只分布在一定域内,实际应用中不会超过该范围,因此式(4)只适用于结构峰值加速度满足该范围内的情况时使用。为克服上述局限性,本文研究中定义φ为振动响应折减系数,表述的物理意义是:在某一振动强度下,行人实际感受到的最大加速度与结构产生的峰值加速度的比值,定义式为

(6)

图5 峰值加速度-振动响应折减系数Fig.5 Peak acceleration-reduction coefficient of vibration response
根据式(6)可得到结构峰值加速度与振动响应折减系数的关系,如图5所示。从图5中可以看出,响应折减系数与峰值加速度之间有一定的相关性,总体上随着峰值加速度的增长,折减系数逐渐减小,但具有较大的离散型。另外,折减系数在分布集中区域分别达到最大值和最小值,这是由于该区域样本数量多,考虑行人荷载的随机性造成了行人实感响应与峰值加速度之间的变异性增大。为便于实际工程应用,同时考虑到结构安全性以及舒适性,建议将振动响应折减系数取为0.8。当然,该取值的合理性还需要大量实验研究。
2.1 改进隶属度函数
隶属度[22]是行人评价振动舒适性的应用基础,由于行人主观反应判断的模糊性以及人对振动敏感程度差异导致的随机性,需要能准确描述不同振动等级的隶属度函数。文献[23]将人体对振动的主观反应划分11个等距感受区间,采用Fechner对数表示隶属度。文献[24]采用指数函数来表示隶属度,认为人体在不同振动响应下的主观反应呈现非等距现象,服从Stevens幂函数定律,试验结果表明改进的隶属度函数能更好地表达振动响应与行人心理量之间的关系。基于上述研究,采用服从Stevens幂函数定律的隶属度函数,即

(7)
式(7)中:vi为第i种主观反应的隶属度;M为采用的判断类别数,这里M取为5,振感等级分为:无振感、稍微感觉到、明显感觉到、不舒适和无法忍受。隶属度与振动等级关系如图6所示。

图6 振动等级和隶属度的关系Fig.6 Relationship between vibration grade and membership
对于连续分布情况下的改进隶属度,隶属度函数表示为

(8)
式(8)中:u为振动加速度响应;umin和umax分别为该环境条件下人主观反应下限和上限所对应的加速度值。
2.2 烦恼率
烦恼率是在某种振动强度下产生烦恼反应的人数与参与实验人数的比例,在离散分布情形下的计算公式为

(9)

基于改进隶属度函数,得到人致人行桥振动烦恼率计算公式,在振动响应连续分布情形下,振动加速度为x的烦恼率计算式为


(10)
式(10)中:σ为标准差,σ=ln(1+δ2);δ为行人感受差异性的变异系数,本文取0.3。
改进烦恼率的计算过程如下,令t=lnu,则


(11)


(12)
A(x)=F1(x)+F2(x)
(13)
式中:

(14)

(15)

(16)

(17)
tmax=lnumax
(18)
tmin=lnumin
(19)
假设RF为舒适度标准规定的反应系数,则umin=RF×0.005,umax=4RF×0.005。不难看出,根据式(10)计算烦恼率的解析解较为复杂,不便于工程应用。经大量拟合分析, 烦恼率曲线采用对数正态分布拟合曲线精度最高,可表示为
A(x)=lncdf(x,μlnx,σlnx)=

(20)
式(20)中:cdf为累积分布函数;μlnx=lnx0.5;x0.5表示烦恼率为0.5时对应的变量x;σlnx=lnx0.841 3-μlnx。烦恼率拟合曲线分布参数及误差如表1所示。
不同使用环境下的烦恼率拟合曲线如图7所示,可以看出,烦恼率计算结果曲线与拟合曲线之间的平均误差均在±1.5%以内,而最大误差不超过3%,表明本文的拟合方法是合理的,采用式(19)近似计算烦恼率曲线能够满足精度要求。

表1 人行桥振动烦恼率拟合曲线分布参数Table 1 Parameters of approximate annoyance curve of vibration

图7 人致人行振动桥烦恼率曲线Fig.7 Annoyance curve of induced-human footbridge vibration
不同变异系数下人致人行桥振动烦恼率曲线如图8所示。由分析可知,当烦恼率值超过0.6后,变异系数为0.1、0.3、0.5三种情形下的烦恼率曲线差异明显,但该烦恼率所对应的振动响应已远超过规定的加速度限值,在实际工程中如此高的加速度响应是不允许出现的。因此,研究变异系数对人行桥振动烦恼率曲线的影响主要分析容许振动响应范围内的,而该范围内的烦恼率曲线基本重合,最大影响不超过1%。

图8 不同变异系数下人行桥振动烦恼率曲线Fig.8 Annoyance curve of footbridge under different coefficient of variation
2.3 烦恼率期望值
由于行人荷载存在个体间及个体内差异,导致结构产生的振动响应在某一域内随机分布[25-26]。为确定人行桥的舒适度,需知道结构在使用环境中的烦恼率期望值。该值为在所有可能的振动强度下产生烦恼反应人数与参数实验总人数的比例,表示为
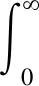
(21)
式(21)中:fX(x)为结构振动响应的分布概率密度函数。
如果已知人行桥峰值加速度的分布概率fa(x),引入振动响应折减系数,基于行人实感下的人行桥烦恼率期望值可改为
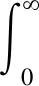
(22)
根据上述分析,本文提出基于行人实感和烦恼率模型的人行桥舒适度评价方法,评价步骤如下。
(1)采用环境激励的自然脉动法对某人行桥进行实验,通过对拾振器采集的加速度信号进行分析,得到结构的竖向主振型自振频率。
(2)测量不同工况下人行桥振动响应,提取每条时程的峰值加速度,得到结构峰值加速度的概率分布,并进行曲线拟合。
(3)通过使用情况确定该人行桥设计系数,结合改进烦恼率曲线以及振动响应折减系数,由式(21)计算烦恼率期望值,评价人行桥振动舒适度。
以荆州市花台人行天桥为例展开实验研究,验证所提舒适度评价方法的合理性。该桥连接交叉路口,为X形悬挂式预制混凝土桥,单跨跨径为12.8 m,桥面净宽1.8 m,路口处共设置4个梯道,全宽2.4 m,净宽2 m,如图9所示。

图9 荆州市花台人行天桥Fig.9 Huatai footbridge in Jingzhou City
为尽可能测试不同工况,时间选择早上和傍晚的高峰段。在跨中位置安装垂直加速度计,并使用INV3018便携式数据采集仪采集振动加速度信号,如图10和图11所示。记录每组工况下过桥人数,人行桥时程响应,并对过桥行人进行舒适度问卷调查。现场试验图片如图12所示。

图10 竖向振动传感器Fig.10 The vertical accelerometers

图11 INV3018数据采集仪和计算机Fig.11 The INV3018 data acquisition instrument and computer

图12 现场实验图片Fig.12 Field experiment
按BS5400舒适度标准,综合考虑环境因素,反应系数取7.5,竖向加速度限值为0.15 m/s2,容许烦恼率规定为20%。不同工况下的人行桥最大峰值响应概率分布如图13所示。由分析可知,该人行桥产生的峰值加速度均小于限值0.15 m/s2,用正态分布曲线拟合峰值加速度反应分布概率的效果最好,分布参数为:μ=0.036,σ=0.024。同时基于不同等级的振动主观感受,统计各振动响应下不同主观反应的人数,根据式(9)可计算出烦恼率实测值。测试工况及计算结果对比如表2所示。

图13 实测响应概率分布Fig.13 Probability distribution of measured peak acceleration
由表2可知,3种烦恼率计算的期望值均小于容许值,与用BS5400方法进行舒适度评价的结果一致,该人行桥动力性能较好,满足舒适度要求。其中,采用结构峰值响应的烦恼率计算结果误差较大,且在LC18、LC37两组工况中计算值超过了烦恼率容许值,与实际情况不符。而考虑行人实感的烦恼率计算值与实测值能较好地吻合,最大误差不超过0.007,验证了所提烦恼率模型的合理性。

表2 振动测试工况Table 2 Vibration test conditions
为解决现行舒适度评价结果过于保守的问题,在已有研究基础上,提出了基于行人实感和烦恼率模型的舒适度评价方法,选取一座已建人行桥进行舒适度评价,得到如下结论。
(1)结构峰值加速度与行人感知的最大加速度具有显著差异,采用结构响应的代表值作为评价指标可能会低估人行桥振动实用性。根据本文定义的振动响应折减系数将二者建立对应关系,可用于估算行人实际感知的最大加速度。
(2)建立合理的舒适度定量分析模型是评价人行桥振动问题的重要手段。本文研究对传统烦恼率模型进行改进,给出了各使用环境下的烦恼率曲线,可供行人激励作用下桥梁振动烦恼率计算作为参考。另外,采用烦恼率期望值进行舒适度评价能够克服现行方法采用单一振动响应所带来的局限性。
(3)基于行人实感和烦恼率模型的舒适度评价方法不仅考虑了行人主观判断的模糊性,同时将感知者的振动加速度作为对舒适度评价的有益补充,较单纯利用结构产生的峰值加速度作为行人感受到的振动响应更具有说服力,推动人行桥舒适性评估向更精细化的方向发展。
猜你喜欢人行行人舒适度基于用户内衣穿着舒适度的弹性需求探讨纺织科学研究(2021年9期)2021-10-14毒舌出没,行人避让意林(2021年5期)2021-04-18改善地铁列车运行舒适度方案探讨铁道通信信号(2020年1期)2020-09-21路不为寻找者而设扬子江(2019年1期)2019-03-08完美 慈善万人行知识经济·中国直销(2018年4期)2018-04-18某异形拱人行桥通行舒适度及其控制研究浙江工业大学学报(2017年5期)2018-01-22我是行人小天使·一年级语数英综合(2017年6期)2017-06-07翻车机人行通道光电安全保护装置设备管理与维修(2016年6期)2016-03-16多跨连拱人行景观桥设计工程建设与设计(2016年8期)2016-03-11浅谈提高奶牛舒适度的方法当代畜禽养殖业(2014年7期)2014-02-27