何国松,董 泽,,孙 明
(1.华北电力大学 控制与计算机工程学院,河北 保定 071003;
2.河北省发电过程仿真与优化控制技术创新中心,河北 保定 071003)
面向国家提出的2030年“碳达峰”的目标,提高以煤炭消耗为主的火力发电厂控制水平,是一种节能降耗的有效方式。而过热汽温系统一直是火电机组热工过程中控制与建模的研究热点,建立高精度的过热汽温模型便于控制器的设计和参数整定。由于过热蒸汽温度系统具有大惯性、大延迟、非线性和时变性等特性,过去常采用的辨识方法有脉冲扰动法、阶跃响应法和频域响应法等,但是这些方法都受限于现场因数,辨识结果存在精度低、通用性差等缺点[1]。近几年随着智能算法的兴起,国内外许多学者采用了粒子群算法,遗传算法、神经网络等许多新型智能算法对电厂过热蒸汽温度控制系统这一类系统进行辨识[2-9]。由于粒子群优化算法对空间探索能力不足,容易陷入局部最优解,同时对非线性问题处理比较困难,文献[10]采用一种基于单位负荷为时变参数的非线性模型(LPVM),与改进的量子粒子群优化算法结合,对现场实际数据进行辨识模型参数,实验结果表明优化后的过热蒸汽温度模型相当精准。文献[11]基于过热蒸汽温度系统的集总参数模型,采用数据库驱动的方法得出过热器出口温度与减温水流量的传递函数,经验证该模型准确度较高。
麻雀搜索算法(SSA)于2020年薛建凯等提出的一种新型群体智能优化算法[12],该算法模拟麻雀觅食和反捕食行为,具有简单、控制参数较少、易于扩充、局部搜索能力强、收敛速度快等特点。由于SSA算法具有不错的搜索能力和开拓能力,近两年来已经有许多学者应用于不同的邻域,吕鑫等人分别将混沌扰动、鸟群算法思想以及传统的大津法融入麻雀搜索算法并应用于图像分割问题,结果表明,优化后的SSA具有收敛速度快,分割精度高等优点,验证了SSA应用于实际问题的可行性[13-15]。文献[16-18]引进聚类的思想,将SSA应用于多目标优化问题与主动悬架LQR控制,提高了多目标求解的均匀性和求解精度,增强了主动框架的控制性能。汤安迪等人使用混沌麻雀搜索算法来规划无人机航迹规划,对比于粒子群优化算法、灰狼优化算法和鲸鱼优化算法(WOA)等,能够以更快速,代价更优地得到一条安全可行航迹[19]。通过以上文献对麻雀搜索算法的改进的研究,虽然在前期全局搜索能力得到一定程度的提高,但是后期还是容易陷入局部最优,且精度不是很高。考虑到量子行为提高了算法的全局搜索能力,但后期可能会出现早熟、收敛现象,混合Lévy飞行策略,当麻雀种群中出现“聚集”或“发散”时对麻雀个体进行适当的调整,使其跳出局部最优,提高算法求解精度。本文对6个基准函数进行测试,并将其应用到控制过热汽温系统辨识问题,验证了该算法有效性与可行性,对提高控制系统控制效果具有现实意义。
1.1 基本麻雀搜索算法(SSA)
SSA算法是模仿自然界一种鸟群麻雀觅食和反扑食行为而提出的一种新型智能群体优化算法,其种群内有着明显的分工,一部分麻雀(发现者)负责为整个种群寻找食物、觅食的方向以及觅食的区域,其余麻雀(加入者)则利用发现者提供的条件获取食物,同时种群内还随机存在侦察者,当其意识到危险时,会及时发出危险信号,整个种群就会立即做出反扑食行为。其中,发现者和加入者角色可以相互交互,但是两者的比例恒定。在SSA中,每一只麻雀代表一个问题的解,麻雀矩阵如下:
(1)
式中:N表示麻雀的种群数,d代表待搜索空间的维数。
发现者一般只占种群数量的10%~20%,其位置更新公式为
(2)
式中:k为当前迭代次数;
i=1,2,…,N,j=1,2,…,d,xij表示第i只麻雀在第j维的位置;
α为(0,1]之间的均匀随机数;
IterMax表示最大迭代数;
L表示[1,1,…,1]1×d的矩阵;
Q为服从N(0,1)分布的随机数;
R2和ST分别表示预警值和安全值,其中R2∈[0,1],ST∈[0.5,1]。当R2小于ST时,周围没有危险,种群中的麻雀未发现有扑食者,引导种群朝着更好的适应度方向搜索。当R2大于等于ST时,侦查者发现捕食者,发出危险信号,整体麻雀向安全区域迁移。
剩余的加入者位置更新公式如下:
(3)

侦察者一般占到麻雀种群数的10%~20%,其位置更新公式如下:
(4)
式中:β为步长控制参数,服从N(0,1)的正态分布;
k为[-1,1]的一个随机数,表示麻雀种群的移动方向;
ε是一个极小的常数,是为了避免分母为0的情况;
fb和fw分别为当前的全局最佳和最差适应度值。当fi大于fb时,表示当前麻雀处在种群的边缘,且容易受捕食者攻击的威胁;
当fi等于fb时,处于种群中间的麻雀意识到危险,需要向其他麻雀靠近,以避免危险。
1.2 混合麻雀优化算法
1.2.1 Lévy策略
莱维分布于20世纪30年代莱维(Lévy)提出的一种新的概率分布,后来经过大量研究表明自然界的许多飞行动物如蜜蜂、果蝇和鸟类的觅食行为都符合莱维分布模式。Lévy飞行是一种结合短距离搜索与偶尔较长距离搜索且服从Lévy分布的随机搜索路径,它能够解释布朗运动、随机行走等自然界中很多的随机现象。Lévy飞行因其能够扩大搜索范围空间和增加种群的多样性,很多群体智能算法使用Lévy飞行更容易跳出局部最优点。由于Lévy飞行模拟十分复杂,到现在为此还没有实现,目前是使用Mantegna算法模拟,生成Lévy随机步长数学表达式为

(5)
式中:β∈[0.3,1.99],σu如下式所示,Γ(Z)是gamma函数:
(6)
由此可得Lévy飞行更新迭代公式为

(7)

(8)
经过多次优化,确定式(8)中Lévy(λ)参数:β=1.5;
步长α=1。
1.2.2 量子策略
使用量子策略改进麻雀搜索算法,使得每只麻雀个体的觅食行为具有量子概率的意义,在转移时没有确定的轨迹和速度,应用该算法可以提升群体智能化程度。应用MonteCarlo方法[20],可以得出麻雀个体迭代时的位置更新表达式:
(9)

(10)


(11)
式中:参数α称为压缩-扩张因子;
mb表示所有麻雀自身最优位置的中心点,由下式确定:
(12)

(13)
对于量子策略迭代后期种群性减少,易陷入局部最优的问题,引入非线性衰减因子,在种群进化过程中,当最优适应值变化较大时,对当前个体进行位置变换;
当适应值变化较小时,采用量子策略进行搜索,对于多个局部极小值的问题,增加全局空间搜索的范围。对(13)式进行改进如下:
(14)

1.2.3 改进算法思想

(15)

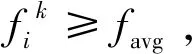


(16)
1.2.4 算法步骤
QSSA算法引入量子策略与Lévy飞行策略,增加种群多样性,避免陷入局部最优的同时提高算法的精度,算法流程图如图1所示,具体实现步骤如下:

图1 QSSA算法流程图Fig.1 QSSA algorithm flow chart
(1) 初始化种群参数,如种群数N,发现者数量dNum,侦察者数量wNum,优化目标维数D,最大迭代次数M,初始值上下界lBound、uBound等。
(2) 计算每只麻雀的适应度fi,并找出最优位置xb、全局最优适应值fb、最差位置xw和全局最差适应值fw。
(3) 选择适应值最优的前dNum只麻雀作为发现者,剩余N-dNum只麻雀作为加入者,分别按照式(8)、式(3) 更新发现者和加入者的位置。再随机选取wNum只麻雀作侦察者,进行预警,再根据式(4)更新侦察者位置。

当fi≥favg时,说明当前麻雀个体呈分散状态,使用式(14)对麻雀个体进行变异,若变异后比之前的个体更优,则采用变异后的个体更新之前的个体,否则保持原最优个体不变。
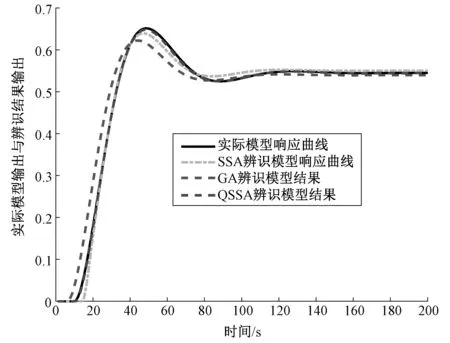
当fi (6)判断当前寻优结果是否满足求解精度或者最大迭代次数,若是,迭代结束,输出结果,否则返回第(2)步。 为了验证QSSA算法的有效性和优越性,在Intel(R) Core(TM) i7-10700 CPU @ 2.90GHz,16.00 G内存,Windows10系统和Matlab R2017a环境下采用6个基准函数进行测试,基准函数如表1所示; 表1 基准测试函数Tab.1 Benchmarking function 设置种群规模为30,最大迭代次数为100,仿真实验中的具体参数如表2所示,基准函数的维数D和初始解的上下限uBound和lBound按照表1选定。为了提高实验结果的可靠性,降低算法随机性带来的误差,每个基准函数独立运行30次,将各个算法的实验数据的平均值和标准差作为最终评价指标,如表 3所示; 表2 各算法参数设置表Tab.2 Parameter setting table of each algorithm 表3 标准测试函数的优化结果比较Tab.3 Comparison of optimization results of standard test functions 表4 标准测试函数的优化时间比较Tab.4 Comparison of optimization time of standard test functions 在热工过程中的系统,一般可以用下面的几种传递函数作为模型辨识的结构: 有自衡对象传递函数: (17) 无自衡对象传递函数: (18) 式中:Tj(j=1,2,…,n)为过程时间常数; fit=∑(y-y0)2 (19) 式中:y和y0分别实际被控对象输出和辨识模型输出。辨识的任务就是寻找最优参数K,Tj(j=1,2,…,n)和τ使目标函数fit最小。 本文基于matlab,将所提出的QSSA算法编写成通用热工过程模型辨识程序,对于单位负反馈系统,步长取1 s,仿真时间取200 s,输入为单位阶跃信号,寻优参数上下限为lBound=[0,0,0,0],uBound=[4,100,100,100]。本次仿真实验所用辨识模型表达式为 (20) 给定QSSA初始参数:种群数量N=30; 表5 QSSA仿真辨识结果Tab.5 QSSA identification results 图2 辨识适应度对比曲线Fig.2 Identify fitness contrast curve 图3 辨识模型响应曲线Fig.3 Identification model response curve 由表5的辨识结果可以看出,使用QSSA算法对模型Gc(s)辨识出来的参数具有随机分布特性,辨识的结果并不唯一,但是从每一次辨识的参数来看,K、T1、T2、τ各个参数的辨识精度都很高。由图2和图3可以看出QSSA很快到达辨识的精度要求,而SSA和GA算法需要迭代到100次才能结束,而且QSSA算法辨识模型的响应曲线几乎与实际模型的响应曲线完全重合,明显优于基本麻雀搜索算法和遗传算法。因此,利用QSSA算法辨识,不仅可以辨识出准确的模型,而且收敛速度快,能够快速的找到全局最优解。 系统辨识要求输入输出数据平稳、正态和零均值,即数据的统计特性与统计时间的起点无关[3]。在生产环境中,由于存在噪声,从现场采集的实际数据通常都包含一些直流或低频成分,使所测数据出现各种漂移或缓慢变化,数据的漂移和趋势变化对系统辨识结果有严重的影响; 为了避免主观意愿和偶然因素,用采集的前2 500个数据进行辨识,后2 500个数据进行模型验证,辨识原始采集输入输出数据如图4所示,图中有较多粗大值并且数据抖动剧烈,本文对实际采集数据采用最小二乘平滑滤波,采用下式进行零均值处理: 图4 原始输入-输出响应曲线Fig.4 Original input-output response curve (21) 式中:N为零初始点个数,一般取4~6个点。 对前3 000个数据进行数据预处理,处理如图5所示。从图中可以看出滤波后的数据不仅剔除了粗大值,而且得到了较好的平滑处理,这样有效的保持了原始信号的真实度。由于过热蒸汽温度控制系统模型具有大惯性大延迟等特性,可以将被控对象等效为[1] 图5 辨识对象数据处理前后曲线对比Fig.5 Comparison of curves before and after data processing of identification object (22) 式中:n为系统的阶次。采用处理后的输入输出数据对模型辨识,本文取n=2,辨识目标精度为0.001,进行5次辨识结果如表6所示。 表6 现场测试数据辨识结果Tab.6 Parameter identification of field test data 由表6可以得出:取5次辨识的平均值作为模型辨识的最后结果: (23) 辨识结果的输出曲线与实际数据的对比曲线如图6所示,辨识模型的输出与实际数据输出的曲线几乎完全重合,同时由后2 500个数据进行模型验证如图7所示。由图7可以看出,辨识模型的输出与后半段实际数据输出的曲线拟合和程度相当高,故由QSSA算法辨识出来的模型相当准确,表明了QSSA算法辨识模型的有效性以及应用于工程的可行性。 图6 过热汽温模型辨识输出与实际数据曲线的对比Fig.6 Comparison between identification of superheated steam temperature model and actual data curve 图7 模型验证结果Fig.7 Model validation results 本文基于麻雀搜索算法存在的缺陷,所提出的混合量子行为麻雀优化算法,不仅提高了麻雀搜索算法寻找全局最优的能力,而且提高了算法的收敛速度和求解精度,并将混合量子行为麻雀优化算法应用于过热汽温模型参数辨识问题。 (1)QSSA在6个基准函数上进行测试,实验结果均能收敛到最优解; (2)通过某600 MW超临界机组过热汽温现场运行数据进行驱动辨识,表明该辨识算法具有速度快、精度高的特点,具有良好的工程应用价值。
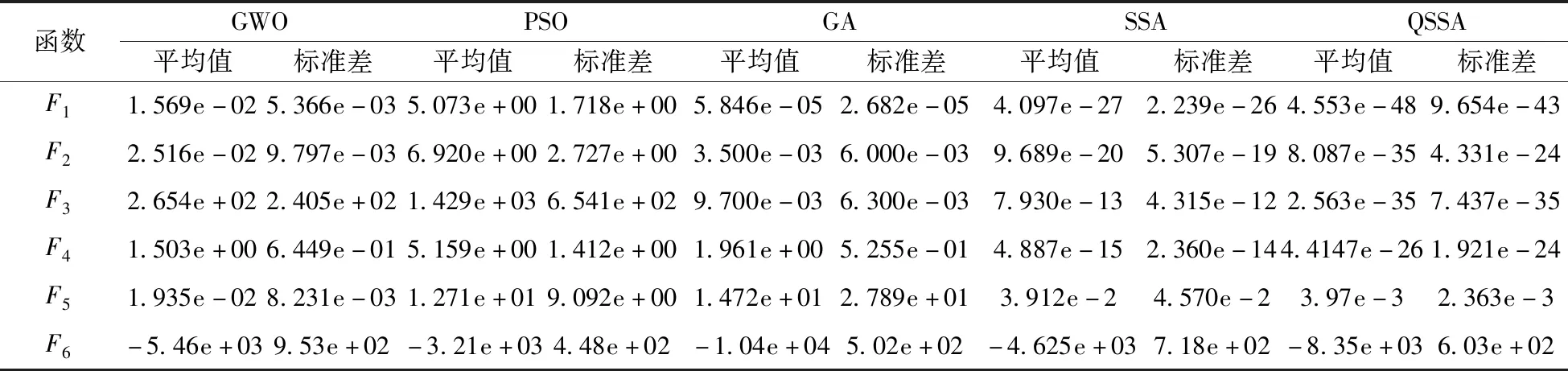
并选取灰狼算法(GWO)、粒子群算法(PSO)、遗传算法(GA)和基本麻雀算法(SSA)进行对比。
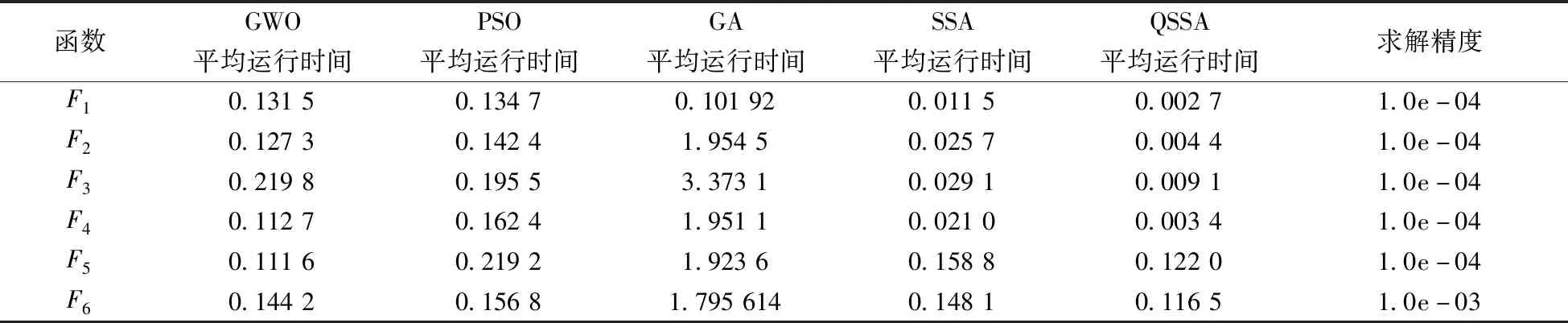
同时参考表3中的标准差作以数量级e-04寻优求解精度(F6取0.001),比较每个算法在不同基准测试函数下独立运行30次的平均运行时间,如表4所示。由表3的实验结果可以看出,LQSSA在寻优稳定性和寻优精度两方面都有优势,相比于其他4种算法都有很大的改进;对于高维单峰函数F1~F4,QSSA算法的多次优化的平均值和标准差都比其他4种算法提高了10个数量级以上。对于F5~F6,QSSA寻优性能比其他4种算法提示不明显,但是在精度和稳定性仍优于其他算法。根据表4的平均运行时间对比结果可以看出,在F1~F4函数优化上LQSSA与GWO、PSO和GA相比,PSO的平均迭代次数减少了97.00%,与基本SSA相比,减少了80.00%。对于F5~F6,LQSSA相比PSO、GA和SSA平均运行时间减少23.17%,LQSSA表现出优良的寻优性能。
K为被控对象对象静态增益;
τ为对象的纯迟延时间;
对于无存迟延被控对象τ为0。采用的目标函数表达式为
发现者PD=20%;
加入者R=1-PD=80%;
侦察者SD=10%;
最大迭代M=100。运行结束条件为t>M或者fobj<0.001。经过5次实验仿真,得到的辨识结果如表5所示。利用SSA、遗传算法做辨识效果对比,适应度曲线和辨识模型输出分别如图2、图3所示。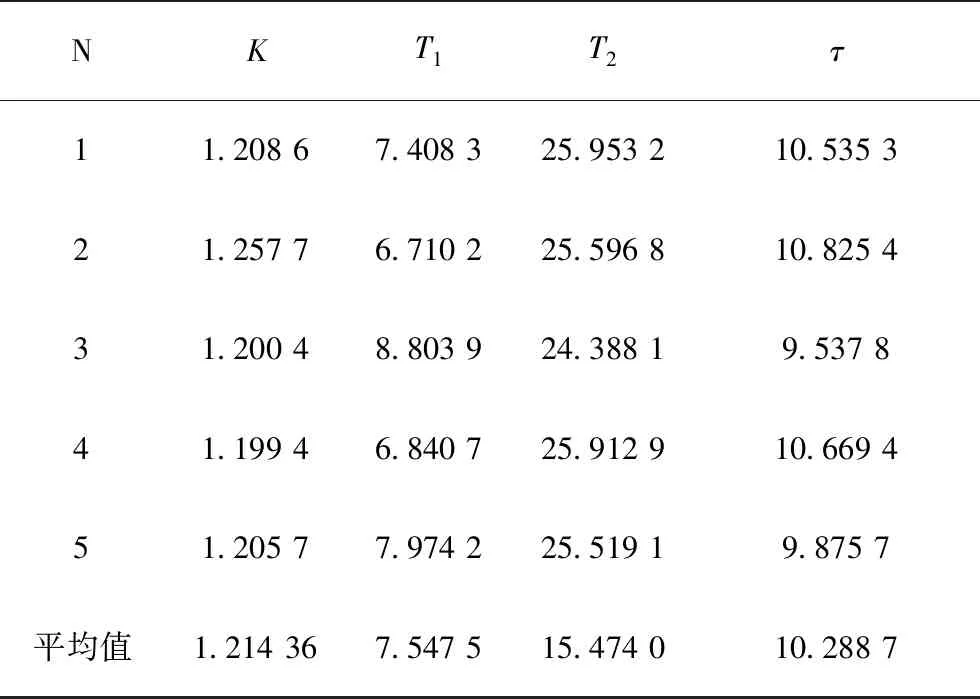

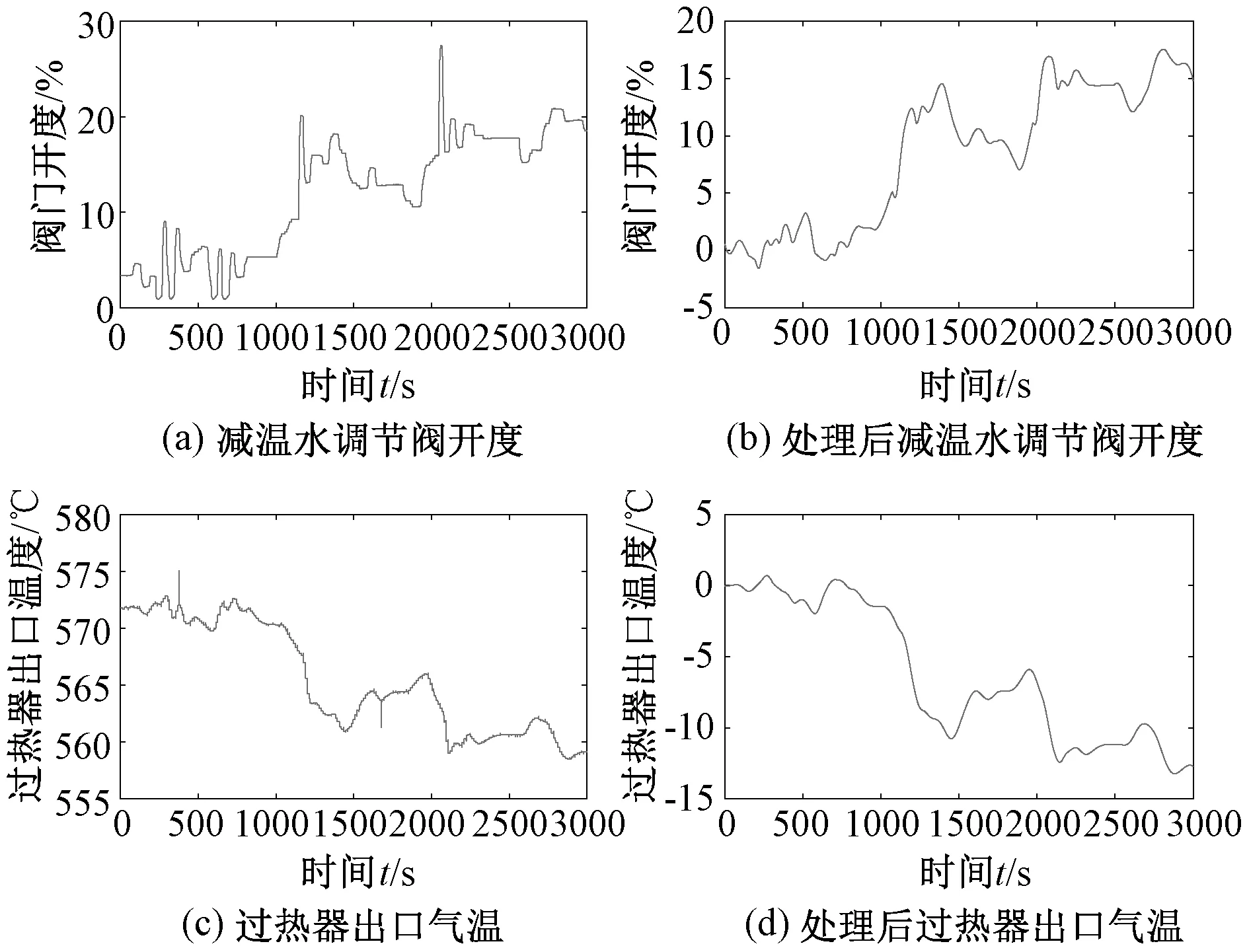
实际采集的未经过处理的现场实际运行数据的“零点”可能是任意的,要想求解与信号零点无关的系统方程,需要找到“零初始值”,然后剔除;
数据采集和传感器等装置短暂失灵会导致采集的数据值远超出实际信号的范围(称此值为粗大值),粗大值会对辨识结果造成相当大的影响。因此需要对数据进行滤波、粗大值和零初始值处理。



相比于GWO、PSO、GA、SSA,运行时间均提升23%以上,寻优精度均提升38%以上,全局收敛性更好。
