丰婉伊,邓晓丽,孙超豪
(1. 武汉轻工大学数学与计算机学院,湖北 武汉 430205;
2. 武汉商贸职业学院信息与工业技术学院,湖北 武汉430205;
3. 华融金融租赁股份有限公司,浙江 杭州 310007)
近年来,4G/5G移动通信技术及智能移动设备的普及,使得移动金融支付的发展迅猛,其支付规模已经处于世界领先地位,有效地降低了金融机构、金融科技公司、单位财务部门等的运营成本并提供更高效的服务[1-5]。随着移动金融支付在金融数据收集和信息新技术方面的发展,需要更加先进和高效的移动金融支付传输属性的数据驱动方法和传输机制来提升移动金融支付的效率和可靠性。
图论为移动金融支付的建模和分析提供了有效的工具。“图”一词直到欧拉的作品问世将近一个半世纪后,才以现在的意义被使用。从那时起,图论成功地应用于各个领域,从传统的结构力学、交通调度到现代网络通信、智能交通、金融数据传输与安全性[3-6]等等领域。
移动金融交易行为是移动终端、4G/5G移动网络和金融支付等方面的组合。在移动金融支付过程中,人们使用数据传输算法保障移动金融支付的数据完整性和准确性。徐嘉营[4]选取智能终端作为移动支付的工具,研究了移动支付将推动家庭金融资产、家庭财富的积累等产生重要的影响,指出了家庭移动支付业务与其它金融产品服务的结合。贺晨霞[5]针对第三方移动金融支付过程中的洗钱犯罪的多元性、犯罪范围的跨区域性和犯罪方式的特殊性等特征问题进行了研究,指出了在移动金融支付过程中应构建一体化的金融监管体系,法律保障体系,指引我国第三方移动金融支付行业在法律体系、金融监管体系下有序、安全和健康地发展。尹志超等[6]研究了移动金融支付对家庭金融资产的影响,结果表明移动金融支付的使用减少了家庭使用货币的需求,提升了移动金融支付的应用。Zhao等[7]针对移动金融支付过程中消费者使用近场通信问题进行了研究,提出了如何较好地使用近场通信完成移动金融支付。针对移动神经网络中的移动端的不同应用场景问题,黄凯凯等[8]在网络的中层提取局部信息和在高层提取全局信息进行融合,建立了网络的移动端场景分类模型,提出了相似类知识迁移的压缩算法,该算法提升了移动神经网络的应用领域。蒋维成等[9]针对移动云计算中给移动任务提供实时保障的问题进行了研究,设计了一种根据任务窗口对虚拟机中的移动任务进行分配的算法,该算法根据移动任务截止期和移动任务窗口大小进行调度分配,确保了在移动任务时延到达内完成,提升了移动资源的利用率。
2.1 图核的计算
图核算法具有完备的数学理论基础,能有效解决高维模型构建问题,已被成功应用于人工智能、生物信息和金融时间序列分析等领域[10-12]。江悠等[10]针对数据间的分布差异、缺少有效整合、影响数据间预测模型等性能问题,提出了一种基于多图核的迁移学习方法,将不同的图核用于挖掘数据结构信息间的可用性与相似性等。图核是度量图对之间相似性的函数[11-12]。它们允许智能学习算法直接在图形上工作。本文的方法结合了Neumann等[13]提出的图核函数,因为这个函数可以在时间线性中计算边的数量。这使得它在实践中具有可伸缩性[9-11]。
首先,每个子图由k阶的Krylov子空间来描述,该子空间是一组向量,来自其截断的幂次迭代[12]。在这项工作中,本文使用k阶Krylov子空间来数学地表示上面生成的子图。k阶Krylov子空间不仅具有有意义的有符号的社会网络的数学嵌入,而且还产生了一些用于稀疏矩阵的最快的线性代数算法。
其次,利用Bhattacharyya核函数度量子图的图核,计算代表k阶Krylov子空间的k维高斯分布的相似度。
利用Bhattacharyya核计算两个k维高斯分布的相似度。对于两个多维高斯分布P1(x)和P2(x),其相似度为
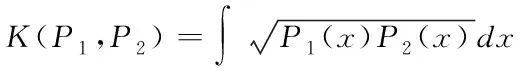
(1)
由于P1(x)和P2(x)服从高斯分布,(1)可以转化为(2)。

(2)
这里,∑1表示P1(x)的协方差矩阵,∑2是P2(x)的协方差矩阵和|·|表示矩阵的行列式。
由于在上述推导的基础上可以用多维高斯分布表示图,因此图G1和G2的相似度可以计算为
S(G1,G2)=K(P1,P2)
(3)
其中P1(x)和P2(x)分别为图G1和G2所对应的多维高斯分布。K(P1,P2)由式(4)计算。
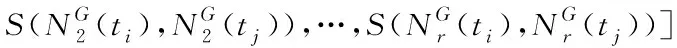
(4)
设D为最短间隔时间预测数据,D={(x1,y1),(x2,y2),…,(xm,ym)},其中xi为(6)计算的第i对用户的相似度,xi∈R,i=1,2,…,m,m为用户数量;
yi是链接的符号,yi∈{-1,+1},-1表示第i对用户之间的链接为负,+1表示第i对用户之间的链接为正。
利用支持向量机,得到
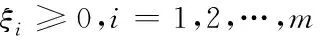
(5)
其中ξi是松弛变量和C是惩罚因子。
利用拉格朗日乘子法得到拉格朗日函数

(6)
通过L对β,ξ和α的导数将得到的方程为零,输出权向量获得β。
2.2 时间拓扑内核
为了提供有效的移动金融支付的可靠性、减少风险,考虑移动金融支付事件之间的时间关系是必要的。现有的图核在文献[14,15]中已经有所讨论,它们主要关注于计算相似的子图结构,而没有考虑它们之间的时间关系[16]。在此,提出了一个时间拓扑内核图。
定义1(时间拓扑内核):让g1=(V1,E1)和g2=(V2,E2)表示节点Pg1与节点Pg2之间的最短路径,从而可以定义时态拓扑内核图

(7)
在Kt是时间子结构内核上定义边缘e1=(u1,v1)和e2=(u2,v2),在节点e1和节点e2上计算时间相似性。
Kt的直觉是基于时间点之间的相似性计算子图结构Kt输入图形之间的递归。如果两个子图是相似的,则它们的节点邻近结构的时间顺序是相似的。对于给定的一对节点v1,v2,其它两个节点ui,uj是相似图g1,g2中到达节点v1,v2的时差。
3.1 移动金融支付结构图
移动金融支付图可表示为一个无向图G=(V,E,T),其中V表示网络中的移动节点集(移动用户、金融机构),E表示无线链路集(数据传输路径),T表示移动节点的金融支付集(支付时间、支付金额)。每个无线链路e=(i,j)∈E代表移动节点i与移动节点j之间的无线链路是直接相连,并且假设无线链路是对称的,即(i,j)=(j,i)∈E。
定义2:图G=(V,E,T)由三个集合组成,一个是移动节点集合,记作V;
另一个是无线链路集合,记作E;
第三个是节点的支付集,记作T。图G中无线链路的两个顶点(vi,vj)的无序节点对是是对称的,即(vi,vj)=(vj,vi)∈E,且vi∈E和vj∈E。
定义3:设无向图G=(V,E,T)的两个移动节点集V与V中节点组成的一组无线链路集E的有限序列。给定一个无向图G的顶点集Vn={v1,v2,…,vn},则节点标记图的数量表示为2(n(n-1)/2)。
设定移动通信网络为无线网络、4G/5G移动网络,M个移动用户(发送者)U1,U2,…,UM(∈V)有n个独立的金融数据c1,c2,…,cn需要传输给N个R1,R2,…,RN金融机构(∈V,接收者)。当发送者Ui(i=1,…,M)进行金融支付时,其金融支付数据经过若干个中间节点Bj(j=1,…,L)传送到Rk(k=1,…,N)接收者,接收者Rk接收到发送者Ui发过来的数据后,进行身份识别、数据交割,并返回交割数据到接收者Rk,完成金融支付数据的传输过程。图1为移动金融支付数据从发送者到接收者的传输结构。
如果发送者(用户)Ui传输数据cj到接收者(金融机构)Rk正确接收的数据量可记为zijk。目标就是

图1 移动金融支付数据的传输结构

(8)
遵循完整内核的框架,保留数据传输的原始拓扑。多核学习(MKL)是将M个指定的核线性组合成一个核K*的过程

(9)
这里,βi≥0,(i=1,2,…,M),β1+β2+…+βM=1.
3.2 移动金融支付的模型
将移动金融支付集表示为一个有向无环图,其中每个金融支付者、金融机构表示一个节点,两个连续的移动金融支付形成一个带有时差(例如,小时)的边,作为它们之间的权重。金融支付的数量可以作为优势权重。
给定n个移动金融支付事件,集合M={(m1,t1),(m2,t2),…,(mn,tn)}表示n个移动金融支付事件,mi表示移动金融支付事件,ti表示mi发生的时间。
图2为基于图核的移动金融支付的数据传输体系。
定义4(移动金融支付图):事件M的移动金融支付图Pg=(V,E)是一个加权有向无环图,顶点V包含所有事件mi∈M,边E包含所有连续事件对(mi,mj)。定义从节点i到节点j的边权值为Wij=tj-ti,定义mi,mj之间的时间间隔。

图2 基于图核的移动金融支付的数据传输体系
给定一个移动金融支付事件,支付时间、支付金额等信息,希望预测该支付的成功或失败。创建了一个时间图G,包括当前支付时间、支付金额等的移动金融支付事件[17,18]。然后,通过考虑以下支持向量机(Support Vector Machine,SVM)的对偶优化问题,在得到的时间图上形成一个二元图分类问题:

(10)
其中K是输入图Gj,Gk上的一个正定图核。C是正则化参数,b是偏置项。给定图形Gi,偏置项b可由

(11)
决策函数定义为

(12)
3.3 移动金融支付子图的构造
为了较好地分析移动金融支付用户(节点)的结构信息,以获得用户的相似性。在无向图G中,节点的结构信息可以用一组子图来表示。某个节点之间最短支付时间的间隔反映了节点金融支付强弱:时间间隔越短,说明节点进行金融支付的程度越强;
时间间隔越远,说明节点进行金融支付的程度越弱。因此,可以利用节点支付时间间隔的时间来控制子图的生成,使得不同子图中的节点具有不同的金融支付强度。首先定义d-hop子图如下:
给定n个移动金融支付事件,集合M={(m1,t1),(m2,t2),…,(mn,tn)}表示n个移动金融支付事件,mi表示移动金融支付事件,ti表示mi发生的时间。

为了对支付信息进行预测,可以用(ti,tj)表示支付信息的路径,可以定义从时间ti到时间tj的一组子图[15]

(13)
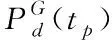
3.4 性能分析
移动用户传送M个分组到N个接收者,每个分组的接收满足二进制概率分布,平均传送M个分组到N个接收者的概率为

(14)
这里,pj是接收者Rj的分组丢失率。
可以通过只包括那些分组丢失率高的接收者来估计上述概率分布。从而可以得到

(15)
这里,p=max{pi},k是分组丢失率高的接收者数量,并且pi=p。
4.1 实验评价参数
在研究中,本文将在计算机上仿真基于图核的移动金融支付质量算法进行评价,其评价性能指标如下:
平均分组丢失率:从源节点发送分组到目的节点,丢失的分组数量除以发送分组的总数据。
平均端到端时延:端到端时延是指分组从源节点传输到目的节点的平均时间。
平均等待时间:平均等待时间是创建和交付任务所花费的平均时间。
平均服务时间:平均服务时间是边缘服务器计算任务的平均时间。
4.2 实验评价环境
在仿真中,本文从湖北金融发展与金融安全研究中心获得了一些仿真用的基础数据,另外通过网络仿真软件NS2[19]对移动金融支付进行实时仿真研究。网络范围可设置为10km×10km,移动终端的发射距离为250m,每个移动终端自由地进行金融支付活动,移动终端按照随机路径点移动模型进行移动,每次模拟执行时间为600秒,移动金融支付的次数在5000次,移动终端的数量为1500以内。在仿真中,设置移动终端的数量为500、1000和1500等三种进行仿真,选择这些仿真运行的平均数据进行分析。
4.3 实验结果分析
平均分组丢失率与移动金融支付的次数具有一定的关系,图3为在移动终端的数量为500、1000和1500个时的仿真。从图中的仿真可以看出,当移动金融支付的次数越多,其数据的传输也就越多,分组丢失率自然也就越高。从图中也可以看出,移动终端的数量越多,其平均分组丢失率也会增多。
平均端到端时延与移动金融支付的次数具有一定的关系,图4为在移动终端的数量为500、1000和1500个时的仿真。从图中的仿真可以看出,当移动金融支付的次数越多,其数据的传输也就越多,平均端到端时延自然也就越高。从图4中也可以看出,移动终端的数量越多,其平均端到端时延也会增多。

图3 平均分组丢失率与移动金融支付次数的比较
平均等待时间与移动金融支付的次数具有一定的关系,图5为在移动终端的数量为500、1000和1500个时的仿真。从图中的仿真可以看出,当移动金融支付的次数越多时,请求支付的数据也就越多,数据的传输、交付任务也就越重,导致平均等待时间也就越高。从图5中也可以看出,移动终端的数量越多,其平均等待时间也会增多。

图4 平均端到端时延与移动金融支付次数的比较
由于移动金融支付的处理是将移动金融支付数据传输到边缘服务器进行支付处理的,从而其平均服务时间是边缘服务器的处理时间。平均服务时间与移动金融支付的次数也是具有重要的关系,图6为在移动终端的数量为500、1000和1500三种情况的仿真。从图中的仿真可以看出,当移动金融支付的次数越多时,请求支付服务的数据也就越多,从而其服务的时间也就越长,导致平均服务时间也就越长。从图6中也可以看出,移动终端的数量越多,其平均服务时间也会增多。

图5 平均等待时间与移动金融支付次数的比较

图6 平均等待时间与移动金融支付次数的比较
4G/5G移动通信技术及智能移动设备为移动金融支付的运营成本和高效的服务提供了重要的技术基础。本文通过构建了一个移动金融支付传输过程的模型,分析了图核的基本理论及移动金融支付传输机制的影响。提出了一种基于图核的移动金融支付传输算法。采取网络仿真的方式生成相应数据,并对相关数据进行分析。研究结果表明,基于图核的移动金融支付传输算法提升了移动金融支付的数据传输率和可靠性。
在移动金融支付传输与处理过程中,还应关注三个方面的问题:一是利用移动边缘计算服务器提升移动金融支付的准确性和快捷性;
二是提升移动智能终端设备的安全与优化传输功能;
三是提升移动金融支付的跨界应用。
