许如宾,杜德琪,蒋婉玥2,,刘晓瑞2,*
(1. 青岛大学自动化学院,山东 青岛266071;
2. 青岛大学未来研究院,山东 青岛266071)
目前机器人应用于各种生产与制造部门,不同的应用对机器人工作空间与灵活性提出了多样化的要求[1]。以电磁兼容测试领域为例,近年来为了应对在电磁干扰(Electromagnetic Interference,EMI)检测与定位等方面的挑战,国内外学术界在合成孔径雷达成像、微波近场扫描等方面进行了大量的研究与研发[2],其研究的重点就是使检测并重建受测系统在空间域中的电磁干扰分布[3],典型案例如美国的双臂测试系统(Large Antenna Positioning System,LAPS)以及NSI-MI公司提出机器人天线检测系统(Robotic Antenna Measurement System,RAMS)[4]等。
在电磁兼容检测过程中,机器人通过抓取检测天线完成对目标辐射源的检测与定位。由于机器人在扫描过程中受测设备辐射特征、检测天线(或探头)极化方向等条件约束,使得机器人的检测/扫描模式会受到自身工作空间可达性的限制[5],这一问题在针对小型电子设备或在紧缩型全波暗室内进行检测时表现得尤为明显。目前对于多关节机器人的运动学求解与路径规划问题研究较多[6],但是对于特定末端姿态约束下的机器人的可达性与灵活性求解方法仍需进一步探索。本文将六轴机器人与微波近场成像(ESM)技术相结合,在给定末端检测天线姿态的前提下,利用对偶四元数法对机器人的空间工作区与灵活性进行了分析讨论,并通过DoE(Design of Experiment)方法提出了对机器人的尺寸与构型优化的方法。以上结果可以为电磁检测方向的机器人选型提供指导,并为扫描控制策略的设计提供依据。
ESM技术来源于合成孔径雷达成像原理[7],主要用于对高速电子设备的电磁干扰(EMI)的检测。在检测过程中,使用多关节机器人抓持探头在空间范围内进行平面或扇面扫描,其系统如图1所示。
在获取了受测设备夫琅禾费衍射区域(距离受测辐射体3~5 λ)内的辐射强度与相位分布后,ESM的成像算法可以通过式(1)表示:
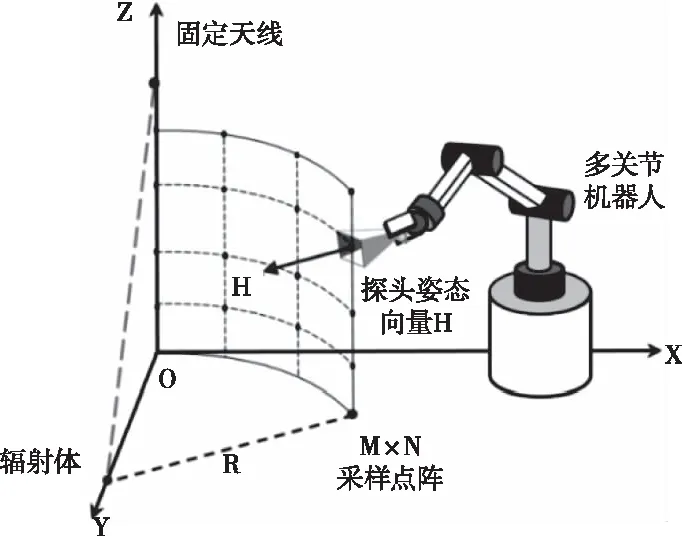
图1 六轴机器人柱面ESM扫描示意图

(1)
式(1)的前提是扫描与电磁辐射源平面都平行于x-y平面,而Z0表示两个平面间的距离。通过在有限空间内采集受测电子设备的平面辐射强度与相位分布,可以同时探测受测设备的表面EMI辐射精度与远场EMI辐射强度。由于近场扫描中探头的极化特征、探头校正等参数是固定的,这就要求对机器人的末端三维姿态给予闭锁(探头姿态H),并在此约束下对机械臂扫描进行规划与控制。
2.1 机器人运动学建模及工作空间分析
本文使用Elfin5型6自由度机器人作为研究与试验对象,其实物及各参数见图2。其中zi指示关节轴线方向,xi,yi与zi满足右手螺旋法则,连杆转角qi表示绕zi轴旋转角度,连杆距离di表示沿zi轴平移距离,ai表示沿xi轴平移距离,连杆扭角αi表示zi绕xi+1轴旋转角度,θi表示各个关节可以自由旋转的角度(1≤i≤6)。据图2所建立的Elfin5机器人结构模型,表1给出D-H参数。

图2 Elfin5机器人结构图

表1 D-H参数表
基于以上构建的运动学模型,将表(1)参数代入,可得正运动学计算公式如式(2)所示。i-1Ti代表坐标系i-1变换到坐标系i的齐次变换矩阵。ScrewQ(r,∅)代表沿Q轴平移r,再绕Q轴旋转角度∅的组合变换,可由D-H表推导得到。
i-1Ti=TRZ(θi)TZ(di)TX(ai-1)TRX(αi-1)
=ScrewZ(di,θi)ScrewX(ai-1,αi-1)
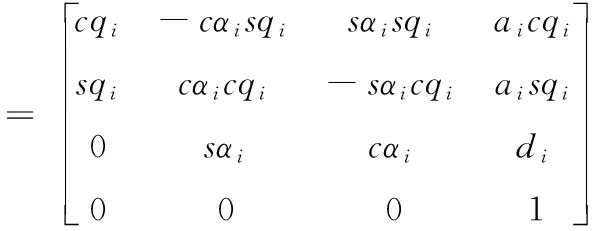
(2)
其中:si=sinqi,ci=cosqi;
基于以上计算,可以求解相对于基座坐标系下末端执行器中点的位姿矩阵0T6,见式(3)。

(3)

(4)
在式(4)中,可以利用左右两侧第3、4列元素之间存在的线性关系求解出运动学逆解。
由于实际应用存在各种物理或软件上的约束,六轴机器人会存在先天的末端不可达区域。本文以ESM天线水平极化方向作为末端姿态约束,以Elfin5机器人的关节限制角度(q2,q3∈[-3/4π,3/4π])作为物理约束条件。在此约束条件下,相对于基座坐标系下末端执行器中点的位姿矩阵0T6保持为沿着基坐标系的x正方向。
在保持给定末端姿态基础上,基于蒙特卡洛法随机取点并代入机器人运动学逆解公式,绘制出机器人末端姿态固定且关节旋转角度受限的可达区域图,见图3。任意选取某一剖面进行可达性分析,其内部存在不可达区域。
通过上述分析,机器人在进行水平极化方向ESM检测时,其工作空间中存在不可达区域。由于机械臂末端执行器的天线极化方向具有对偶性,本文只针对水平末端姿态这一约束条件进行分析。下文将对不可达区域进行建模分析。
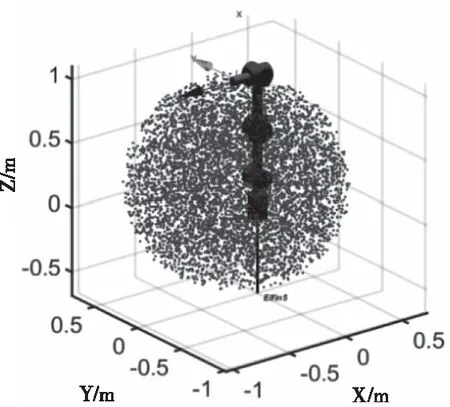
图3 利用蒙特卡洛法确定的可达区域
2.2 不可达区域的建模
前文对机器人逆运动学已经进行求解,部分结果如下
q3=arctan2[(ks23-hc23)/a2,(kc23+ns23+d4)/(-a2)]
(5)
式中
s23=sin(q2-q3),c23=cos(q2-q3)
k=d6az+d1-pz
h=-d6axc1-d6ays1+pxc1+pys1
n=-d6axc1-d6ays1+pxc1+pys1
从式(5)可知,第三关节的旋转角度与空间中的任意点(px,py,pz)存在映射关系。本文在确定px=-0.13m,平行于YOZ的平面上密集取点,绘制该平面上第三关节旋转角度,其中纵坐标轴代表各点的第三关节的角度,见图(4)。
图4表明:该平面上第三关节角度以某一点为最小值且第三关节角度梯度呈圆环状向外扩散而缩小,该平面上不可达区域为圆形。由于机器人运动过程中存在物理约束,在图4中表现为第三关节角度小于-153° 的区域是不可达区域。对px取不同值分析,发现不同取值下的不可达区域都为圆形,故推测不可达区域为球形区域。对不可达区域的三个坐标轴进行分析,确定三视图边界各点取值并进行最小二乘法拟合,最终确定的圆心及半径数据见表2。

图4 剖面上第三关节旋转角度
设最小二乘圆的方程如式(6)所示,令残差项如式(7)所示
x2+y2+ax+by+c=0
(6)
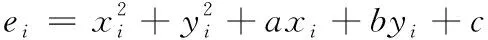
(7)
基于以上设定,模型如式(8)所示。模型中F的偏导数必须满足最小化条件如式(9)所示。设圆心坐标为(A,B),圆的半径为R,则R如式(10)所示
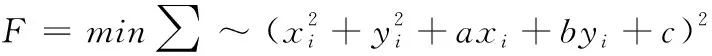
(8)
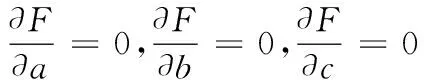
(9)

(10)
由此,可以得到机器人不可达区域的边界拟合图,如图(5)所示。
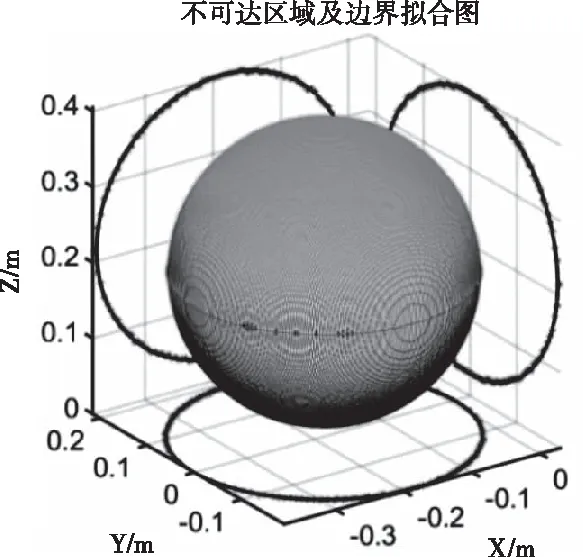
图5 不可达区域三视图边界拟合

表2 边界拟合圆心及半径
从拟合结果看,不可达区域可以在一定的误差允许范围内当成球体,下面验证该结论的准确性。为了方便进行验证,做出如下近似取值:球心O(-0.185,0,0.215),半径为R。按照一定的步长选取不同的半径R,均匀地在球面上取点并遍历,判断是否满足条件q3≤-153°,确定满足条件的点的个数,绘制出图(7)中A曲线。再绘制出(1000R)2的曲线,见图6a中曲线B(图6b为图6a中黑圈部分的放大图)。
从图6中可以发现,两条曲线在R=0.2m附近出现重合,结合局部放大图进行分析,可以证明在一定误差允许前提下,认为该不可达区域为球体,半径R=0.196m。

图6 机械臂不可达球域随采样点数的变化趋势
本小节可以说明,在保持机器人末端姿态固定的情况下,其工作空间内部存在不可达球域,且该不可达球域与机器人物理约束相关。
2.3 对不可达区域边界尺寸的证明
参照D-H参数确定过程,将绕z轴旋转量q,沿z轴平移量d,绕x轴旋转量α,沿x轴平移量a的坐标间的变换用对偶四元数表示为
i-1i-1
(11)
其中
由此得到对偶四元数变换方程如式(12)所示,对式(13)进行变量分离,可得式(15)。
112233445566=
(12)
(13)
1=u1+u2i+u3j+u4k+ε(u5+u6i+u7j+u8k)
(14)
(15)
根据对偶四元数对应相等,可以知道ui=vi,uk=vk(i=1,2,3,4;
k=5,6,7,8),得到
Dj=EjRj=1,2
(16)
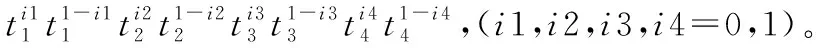
根据矩阵对应相等,取式(16)前4个方程。
x1=cos(q5/2)cos(q6/2)
x2=sin(q5/2)cos(q6/2)
x3=cos(q5/2)sin(q6/2)
x4=sin(q5/2)sin(q6/2)
求解后将这4个量代入式(16)的后4个方程。
gk(t1t2t3t4)=0k=1,2,3,4
(17)
(18)
G1(w,a,y,z),G2(w,a,b,z) ,G3(w,a,b,c)
将式(18)展开得式(19)。
δ=MD6×6NT=0s.t|D6×6|=0
M=[a2b,ab,b,a2,a,1]
N=[z2y,yz,y,z2,z,1]
(19)
矩阵D6×6为只含有w的矩阵,即Dixon矩阵。代入具体数值后矩阵D6×6每行分子分母关于变量w的最高次数为[4,0,0,4,0,0],总和为8,即该机器人一共有8组逆解。
通过对本小节的分析可知,前文已求出全部8组逆解,并不存在漏解情况,证明求出的不可达区域是最小不可达区域。
DoE是一种实验设计的方法,通过对输出参数的量化分析,寻找最关键的因素[10]。本节采用全因子设计法来分析各种因子对半径R的影响程度。根据式(20)可以将式(5)进行简化,并表示为式(21)。

(20)
R=f4(d1,d4,d6,a2,ax,ay)
(21)
据式(23)影响半径R的因子共6种,对每种因子采取两水平测试,进行64次试验,记录下各因子不同水平半径R的值,进行全因子分析。因子作用表示单个或多个因子共同作用,p值小于0.005代表该作用项为显著作用项,对半径R起关键影响。部分结果如表3所示。
通过表3可知作用较为明显的因子共三项,故选择d4和a2作为显著作用项,绘制出R的等值线图7。将全因子分析得到的数据进行拟合分析,得到半径R与因子之间的关系式(22)。
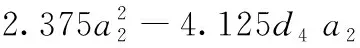
(22)
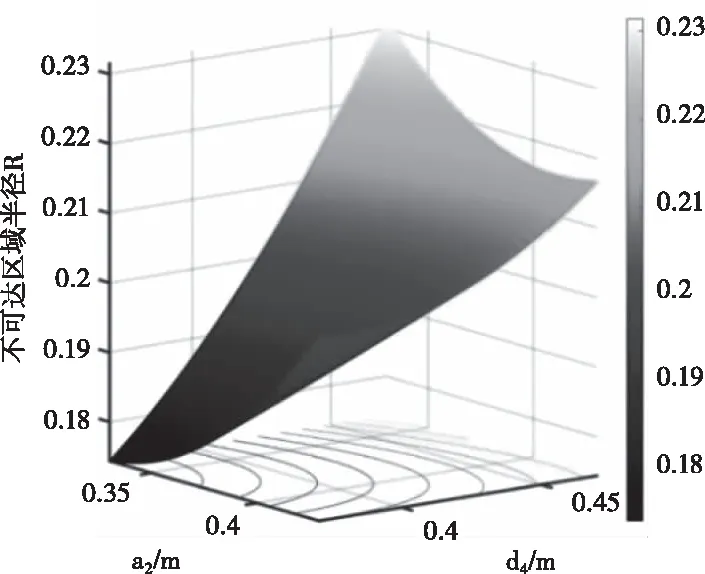
图7 a2 与d4 作用下不可达球域半径R

表3 不同因子作用下的P值
综上所述,其余因子取值确定且合理的前提下,不可达球体的半径R与d4和a2的取值呈正相关,且d4对半径R的影响权重略大于a2。对于进行平面扫描机器臂参数选择时可以优先考虑d4和a2这两个因素,且这两个参数应尽可能小,以实现不可达区域最小化的目标。
基于以上分析结果,在ESM机器人进行柱面扫描时,需要先确定柱心坐标O(x,y)和底面半径r,再确定相对于基座坐标系下末端执行器中点的位姿矩阵0T6。柱面扫描要求机器人末端中心与待扫描件包络柱面垂直且平行于平面。利用圆的性质及三角公式,可以得到0T6的具体表达,如式(23)所示。

(23)
式中
ax=-px/r
ay=-py/r
ox=cos(π/2+theta)
oy=cos(theta)
其中theta=arctan(py/px)表示待扫描点与基坐标x轴正方向夹角,该参数用以表征机械臂扫描过程所处的位置。
以固定步长遍历作为柱心坐标,分别以不同的半径构建圆柱体并均匀取点。圆柱表面上的点即对应位姿矩阵0T6中的坐标点(px,py,pz)。测试各柱心坐标下不同半径对应点集是否可达并记录下最大值,绘制出图(8)。
综合本小节上述内容,图中曲线C是X=-0.2m处的曲线,柱面上可达点较大值都出现在曲线C上,在曲线上总体呈现先增加再减小的趋势,通过剃度便利,可以在O(-0.2,-0.1)处取得柱面扫描可达点的最大值。

图8 柱面扫描下可达点集
针对应用于电子设备EMI的机械臂扫描系统的要求,提出了针对特定末端姿态约束下的机械臂工作边界的确定及评估方法。为了求解在指定机械臂末端姿态(天线极化方向)约束条件下的机械臂可达性,本文在D-H模型的基础上利用蒙特卡洛法分析末端执行器的工作空间,并证明该空间存在一个不可达球域。本文采用对偶四元数方法同时优化了对系统的动力学模型逆解的求解,最终得到了机械臂不同运动参数对该不可达球域尺度的影响权重。以上分析方法在Elfin5六轴机械臂上进行了检验,证明可以在给定末端姿态的条件下提供机械臂的最优参数选择方案,为电子系统ESM扫描系统的设计控制提供依据。
猜你喜欢运动学姿态半径攀爬的姿态学生天地(2020年3期)2020-08-25基于MATLAB的6R机器人逆运动学求解分析河北省科学院学报(2020年1期)2020-05-25工业机器人在MATLAB-Robotics中的运动学分析重型机械(2019年3期)2019-08-27连续展成磨削小半径齿顶圆角的多刀逼近法制造技术与机床(2019年6期)2019-06-25基于D-H法的5-DOF串并联机床运动学分析制造技术与机床(2018年11期)2018-11-23全新一代宋的新姿态汽车观察(2018年9期)2018-10-23跑与走的姿态中国自行车(2018年8期)2018-09-26一些图的无符号拉普拉斯谱半径华东师范大学学报(自然科学版)(2017年1期)2017-02-27基于运动学原理的LBI解模糊算法海军航空大学学报(2015年1期)2015-11-11热采水平井加热半径计算新模型中国海上油气(2015年3期)2015-07-01