梁鸿宇,刘百川,马芳武,王登峰
(吉林大学,汽车仿真与控制国家重点实验室,长春 130022)
点阵结构仿生于自然界中的动植物微观特征,按照特定的排布规则重构而成[1-4]。由于其天然的轻量化特征与优异的比吸能特性,在工程领域得到广泛关注。在双碳政策与新能源汽车碰撞安全的驱动下,三维点阵结构凭借更高的结构利用率,成为近几年的研究热点,被国内外公认为新一代先进结构材料[5-6]。研究汽车多角度碰撞载荷下点阵结构吸能部件的选择依据与设计策略具有重要意义。
当前,点阵结构多填充于薄壁管中形成一种组装式结构,可以兼具承载与吸能能力[7-8]。在早期的应用探索中,学者们以负泊松比点阵结构为研究对象,侧重于点阵结构设计参数对吸能盒轴向耐撞性能的影响。张伟等[9]系统地研究了双箭头负泊松比结构的轴向压缩特性,对平台应力的增强效应与产生机理进行了详细阐述,并将其应用在汽车吸能盒中,在满足性能需求的前提下,减质量44.4%。进一步地,周冠[10]对比分析了传统吸能盒、泡沫铝填充吸能盒以及双箭头点阵结构填充吸能盒的耐撞性能,结果表明:这种新型吸能盒结构具有更优异的吸能能力,可以显著提升汽车的安全性能。王陶[11]将三维内凹六边形负泊松比点阵结构填充于汽车吸能盒中,采用数值模拟的方式研究这种新型结构的吸能特性,研究结果表明:相比于传统吸能盒,这种填充式吸能盒具有更加全面和优异的耐撞性能。Wang等[12]基于人体骨骼的构型,将吸能盒本体内部填充的内凹六边形负泊松比结构进行功能梯度设计,使峰值冲击力与比吸能均得到提升。考虑到实际碰撞工况中斜向冲击的普遍性,马芳武等[13]进一步研究了内凹六边形负泊松比点阵结构在0°-30°冲击角度范围内的耐撞性能,证实了冲击角度对负泊松比点阵结构的内聚效应以及填充式吸能盒的吸能稳定性具有显著影响。综上,现有研究关于点阵结构填充式吸能盒在多角度冲击载荷下的影响机制尚不清晰,一方面,缺乏点阵结构内芯的选择依据,另一方面,过于关注点阵结构内芯的设计与优化,忽略了吸能盒本体设计对性能提升效果的限制影响。
基于上述的研究局限性,本文中以点阵结构填充式吸能盒为研究对象,选取4 种典型点阵结构作为填充芯体,研究不同工况加载下点阵结构填充式汽车吸能盒的吸能特性,阐明点阵结构与吸能盒本体的相互作用机理及内芯选择依据。基于Ma 等[14]前期开展的点阵结构填充吸能盒优化研究,分析优化前后的性能提升效果,针对设计不足提出了吸能盒本体改进方案。基于改进本体结构的点阵结构填充式汽车吸能盒进行抗撞性多目标优化设计,阐明本体设计对性能提升效果的重要影响,并对优化结果进行验证。该研究对填充式吸能部件面向多载荷工况性能需求的设计具有重要的指导作用。
对吸能盒结构的耐撞性分析涉及的评价指标定义如下。
(1)综合比吸能SEAθ
综合比吸能为各冲击工况下比吸能的加权值,重点考察结构的综合抗撞性,其定义为
式中:SEAθk为某一冲击角度θk(k=1,2,…,Nθ)时的比吸能值;
Nθ为考察的角度冲击工况数量,一般考察范围为0°-30°,以5°为间隔,共7 种角度工况,即0°、5°、10°、15°、20°、25°和30°工况;
ωθk为冲击角度θk的权重值,因为本文重点分析结构的耐撞性能影响机制,不考察由于交通场景差异性引起的权重变化,所以采用等权重准则进行权重分配[5]。
(2)吸能稳定性σE
吸能稳定性σE主要考察角度工况变化时比吸能特性的波动情况,以衡量耐撞性能的稳定程度。
式中μ为所有考察工况下比吸能值的平均值。
(3)峰值冲击力Fp
峰值冲击力Fp为结构变形吸能过程中所产生的最大反力,该值应尽可能小,防止造成瞬间的致命损伤。
在考察多角度工况时,该值为所有工况下的全局最大值,无需进行加权计算。
(4)平均碰撞力Fav
有时也会采用平均碰撞力Fav对结构的平均抗撞性水平进行评价,在考虑多角度工况综合性能时,可以如式(5)进行加权计算。
式中:Ea为结构变形吸收总能量;
D为冲击行程。
2.1 吸能盒本体结构与4种点阵构型
如图1 所示,本文选择某车型的钢制吸能盒作为设计参照。为便于后续的对比分析,对该结构进行简化处理获得吸能盒本体结构,其总体尺寸为235 mm×128 mm×75 mm,壁厚为1.5 mm。本体结构在上、中、下位置沿周向各分布4 处半圆形诱导槽。其中,中部的诱导槽位于吸能盒的最中间位置,宽10 mm,高3 mm。位于上部与下部的诱导槽距离中部诱导槽95 mm,其宽和高分别是15 和2 mm。此外,各诱导槽距离外壳边缘9 mm。
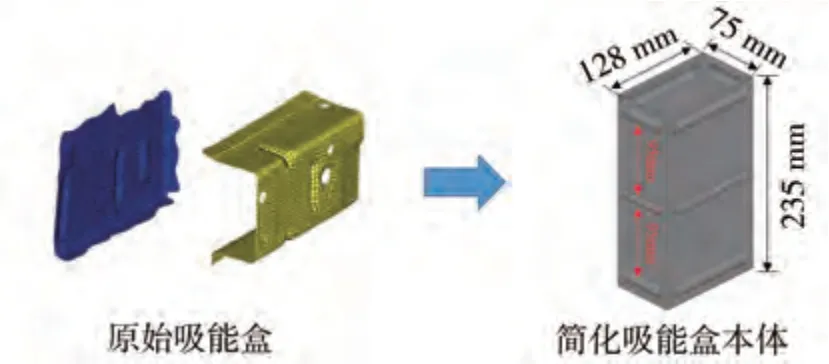
图1 吸能盒本体结构及其分析简化模型
同时,选取了4 种典型的点阵结构进行微观胞元的模拟。图2 给出4 种典型点阵结构的二维代表性单元及三维点阵的演化过程。以六边形结构(hexagonal structure,HS)为例,将二维六边形结构旋转90°,即可得到正六边形三维点阵代表性胞元,然后沿3 个正交方向进行若干胞元规模的阵列,形成正六边形三维点阵结构,其他3 种结构也是同样的演化思路。这里需要说明,选择这4 种点阵结构进行方案选择的原因主要是这4 种结构无论在二维还是三维点阵形态下的耐撞性研究中都较多,均已被证实具有优异的性能表现。学者们常按照泊松比效应进行分类,将六边形点阵结构作为正泊松比结构的代表,将其他3 种点阵结构作为负泊松比结构的典型代表。

图2 4种典型点阵结构的二维代表性单元和三维点阵的演化过程
进一步地,根据图1 的结构表征,正六边形结构HS、内凹六边形结构(re-entrant structure,RS)、星型结构(star-shaped structure,SSS)的胞元均可以采用倾斜胞壁长度l、水平胞壁长度h、胞壁厚度t以及角度γ进行表示。双箭头结构(double arrowhead structure,DAS)的胞元可以由倾斜胞壁长度l、厚度系数η、长度系数λ、比例系数K、角度φ和γ进行表示。其中:厚度系数η为胞壁厚度与胞壁长度之比;
长度系数λ为水平胞壁长度N与胞壁长度L之比;
比例系数K为短胞壁长度M与长胞壁长度L之比。基于单胞法[9-11],推导了这4 种三维点阵结构的相对密度公式:
关于点阵结构填充吸能盒的模型组装,按照如下步骤确定:首先基于点阵结构相对密度一致,确定各元胞结构参数,本文所用结构参数如表1 所示;
再结合吸能盒本体结构的总体尺寸,确定填充规模。

表1 三维点阵填充结构的结构参数
2.2 有限元模型的建立
采用LSDYNA 进行有限元仿真模型的建立与计算。如图3 所示,以正六边形点阵结构填充吸能盒的模型效果图为例进行仿真设置说明。采用壳单元对吸能盒本体结构进行网格划分,网格尺寸为5 mm。材料采用钢材,用MAT24 分段线性塑性材料模型进行表征,材料参数为:弹性模量Es=210 GPa,密度ρ=7850 kg/m3,泊松比λ=0.3,其真实应力-真实塑性应变值如表2 所示[14]。考虑到应变率对屈服应力的影响[15],采用Cowper-Symonds 准则进行表征,其中应变率系数C=100 s-1,p=10。三维点阵结构采用梁单元进行模拟,通过网格收敛性分析[14],兼顾计算精度与计算效率,将网格尺寸确定为1 mm。考虑到汽车轻量化的需求,材料选用铝合金材料[14],用MAT3理想弹塑性材料模型进行表征,其材料参数为:弹性模量Es为71 GPa,质量密度为2 810 kg/m3,屈服应力为325 MPa,泊松比为0.33,由于铝合金对应变率不敏感,本文不考虑其应变率效应。

表2 真实应力σt 与真实塑性应变εp

图3 点阵结构填充式吸能盒有限元模型与加载条件
将点阵结构置于吸能盒本体内,底端固定在下方刚性墙上,再由上方刚性墙进行加载。根据文献[7],冲击刚性壁的附加质量设置为1 000 kg,冲击速度基于分析需求而定,冲击角范围设置为0°~30°。接触设置方面,点阵结构与吸能盒本体结构分别设置自接触模式,点阵结构与吸能盒本体之间、刚性墙与点阵结构之间、刚性墙与吸能盒本体之间分别采用面面接触,所有静摩擦因数设为0.3,动摩擦因数设为0.2。这里需要说明的是:考虑吸能盒的实际安装情况,冲击刚性墙沿吸能盒宽度方向进行加载。
2.3 仿真精度验证
为更加直观地验证仿真模型的可靠性,以正六边形点阵结构填充吸能盒轴向冲击工况为例,将冲击速度设置为54 km/h,使整体结构完全压实,观察整个冲击过程中的能量转化曲线及其变形模式[7]。如图4 所示,可以看到结构整体呈现逐层压溃的稳定变形模式,每一时刻下结构吸收的动能量均等于内能增加量,沙漏能与滑移能之和远远小于内能的5%,总能量基本维持不变。综上,可证实仿真方法的准确性与可靠性[13-14],以用于后续的分析评价。

图4 结构变形过程中的能量转化曲线
3.1 综合耐撞性能分析
表3 所示为不同点阵结构填充吸能盒的综合耐撞性能。值得注意的是:3 种负泊松比结构在任一综合指标下都较为相近,这意味着负泊松比填充吸能盒结构可能具有某一共性的机理性特质。同时,在吸能性方面,可以清楚地看到:相对于其他3 种负泊松比结构填充吸能盒,正六边形点阵结构填充吸能盒不仅单位质量的综合吸能量最高,且随角度工况波动下,具有很好的稳定性;
在最大冲击力方面,正六边形点阵结构填充吸能盒也是4 种结构中最大的。这意味着正泊松比点阵内芯结构与负泊松比点阵内芯结构之间存在吸能机理上的不同。

表3 不同点阵结构填充吸能盒的综合耐撞性能
综上,进一步对正、负泊松比填充结构的变形机理进行对比分析,以揭示耐撞性能的影响机制。
3.2 影响机理分析
如图5 所示,将传统无填充内芯的吸能盒本体的综合比吸能与吸能稳定性作为空白对照。由图5可见:本体结构自身的吸能效率就可达到10 996 J/kg,相比之下,3 种负泊松比点阵结构填充吸能盒的吸能效率并没有得到明显提高。相反,正六边形点阵结构内芯的引入使吸能盒结构的吸能效率增加了18%。为清楚地解释这一现象,以正六边形点阵结构填充吸能盒与3 种负泊松比点阵结构填充吸能盒的轴向压缩变形过程为例,进行更加直观的阐述,如图6 所示。可以看到:由于负泊松比结构具有压缩收缩特性,在吸能盒压溃过程中,内芯向内收缩,导致内芯与本体之间的相互作用减弱,不利于产生耦合增强效应;
相反,正泊松比结构在压溃过程中向外膨胀,促进了其与本体之间的相互作用,因此导致了结构整体的吸能效率大幅提升。

图5 不同吸能盒结构的耐撞性能分析

图6 正、负泊松比点阵结构填充吸能盒的变形机理图
通过图5可以进一步观察到:4种点阵结构填充吸能盒在吸能稳定性方面,均要优于传统无填充内芯的本体结构。这主要因为在角度冲击下,吸能盒结构会发生弯曲变形,不再保持轴向冲击时的渐进压溃模式,因此吸能效果会降低;
而对于点阵结构填充吸能盒来说,角度冲击会增加内芯与本体之间的相互作用,一定程度上可以抑制整体结构的过度弯折。为直观地说明,图7 展示了传统无填充内芯的吸能盒本体结构与不同点阵结构填充吸能盒在角度冲击下的变形模式图。从图中可以看到:相比于传统吸能盒,在角度冲击时,由于内芯结构的存在,整体结构的弯曲程度得到改善,在20°冲击工况时最为明显。同时,3 种负泊松比点阵结构填充吸能盒在各工况下的变形模式基本相同,这与上述综合性能指标的分析相一致。而在小角度冲击工况下,可以明显地看到正泊松比点阵结构与本体之间产生的压缩膨胀行为。基于文献[14],通过对内芯进行优化设计,在大角度冲击工况下可以实现40%~50%的性能增益,但无论如何对内芯进行优化,在30°工况时,点阵结构填充吸能盒均在最下端诱导槽处发生弯折现象(见图7(b)),因此启发我们:吸能盒本体的设计将会制约角度冲击时性能提升的优化效果,不应过多关注于内芯的设计,应对本体结构进行预先的优化调整,否则会极大影响到大角度冲击下的吸能效果。为对上述分析进行直观验证,将在第4 节多目标优化设计中做具体说明。

图7 填充前后吸能盒角度冲击下的变形模式
3.3 耦合效应分析
如图8 所示,展示不同点阵结构填充吸能盒在多角度工况下各组成部分的吸能量,来阐述上述变形机理对耦合效应的影响。首先,可以观察到:随着冲击角度的增加,由于结构逐渐由渐进压溃变形向整体弯曲变形转变,填充吸能盒的吸能量呈下降趋势。但是无论是轴向冲击还是斜向冲击,点阵结构填充吸能盒的吸能主体仍是吸能盒本体,这主要是因为独立的点阵结构在没有四周约束的情况下,会出现结构失稳现象,所以其吸能量较小。如若增加点阵结构的壁厚会增加吸能性,但会显著增加吸能盒的质量,不利于轻量化效果,因此填充点阵结构的壁厚一般较小。相比之下,点阵结构与本体之间的耦合效应更值得关注。可以观察到:轴向冲击工况下,HS填充吸能盒由于正泊松比效应引起的压缩膨胀,促进了结构之间的相互作用,因此其耦合效应产生的吸能量要大一些。随着冲击角度的增加,HS 填充吸能盒在各工况下的耦合效应均是最大的,且耦合效应产生的吸能量在斜向冲击工况下要比轴向工况更加明显,这主要是因为斜向冲击下增加了点阵结构与本体之间的接触面积。综上,从综合耐撞性指标、变形影响机理及耦合效应能量分析,揭示了点阵结构填充吸能盒的吸能影响机制,为点阵结构的选择及本体设计提供了实际依据。

图8 不同点阵结构填充吸能盒在多角度工况下各组成部分的吸能量
3.4 内芯选择依据的阐述
上述对点阵结构内芯及本体的作用机理进行相应说明。基于此,可以对点阵结构填充吸能盒的内芯选择依据作如下总结:
(1)对于小角度冲击工况为主要应用场景的使用需求,应尽量选择正泊松比点阵结构作为填充内芯,充分利用耦合增强效应,在较短时间内吸收大量动能。
(2)对于峰值力指标比较敏感的使用需求,可考虑应用负泊松比点阵结构作为填充内芯,但需要对吸能盒本体上的诱导槽结构进行设计考量,加强耦合作用,以确保吸能目标的达成。
在上节提及本体设计对点阵结构填充吸能盒的重要性,尤其在大角度冲击工况。因此本节将率先针对本体结构进行改进设计,再基于改进本体结构的点阵结构填充式汽车吸能盒进行抗撞性多目标优化设计。
4.1 吸能盒本体的改进设计
对本体结构提出了更高要求。首先从轻量化效果考虑,由于铝合金具有更高的比吸能性,因此采用铝合金材料代替钢材;
其次在性能方面,在中低速角度冲击工况下(16 和48 km/h,0°~30°),希望点阵结构填充式吸能盒均可具有优异的耐撞性能,对壳体长宽比以及其上分布的诱导槽形状、数目、位置、尺寸展开对比研究,为点阵结构填充式吸能盒提供性能优异的本体结构。
如表4 所示,在保证壳体结构的总面积及截面周长一致的前提下,考虑布置空间,提出了4 种比例的长宽比构型,即4∶1、2∶1、4∶3、1∶1。

表4 壳体不同长宽比构型的示意图
针对上述4种长宽比构型,对16与48 km/h两个冲击速度下的7 个冲击角度工况(0°、5°、10°、15°、20°、25°、30°)进行仿真模拟。在各工况权重设置方面,考虑吸能盒的应用场景,低速冲击工况作为重点关注工况占80%,中速冲击工况占20%。此外,各冲击速度工况下的角度按等权重分配。主要对比吸能SEAθ-LM、平均压溃力、低速时的最大峰值力、吸能稳定性等性能指标进行综合评价,指标中的θ代表冲击角度;
LM 代表低速工况与中速工况,即综合工况。
表5 给出不同长宽比构型的综合性能指标值。可以发现:在等质量条件下,随着宽度尺寸逐渐增加,其综合吸能性以及平均压溃力均呈现递增规律,峰值冲击力相同,吸能稳定性大幅提升。究其原因主要是当宽度增加时,使整体结构在角度冲击工况下沿受力方向上的刚度得到加强。与此同时,也增加了横向的变形空间,使结构的整体弯曲行为得到显著改善。综上所述,将最佳的截面长宽比选为等比例形式,即1∶1。

表5 不同长宽比构型的综合性能指标值
按照以上分析步骤,依次对本体上的诱导槽分布特征进行对比研究,获得了最终的改进本体结构形式如下:本体截面长宽比为1∶1,其上分布2 个4 mm 的方形诱导槽,第一诱导槽的位置在距离顶端水平面的85.67 mm处,第二诱导槽的位置在距离顶端水平面的171.82 mm 处。由于篇幅有限,对分析结果不作详细展示。
4.2 抗撞性多目标优化设计
以改进后的壳体结构作为点阵结构填充式吸能盒的本体结构,进行进一步的优化设计,并对性能优化效果进行考察。
4.2.1 优化目标的确定
本次优化以点阵结构的结构参数与本体壁厚作为设计变量,目标性能值为综合比吸能、综合平均碰撞力、峰值冲击力,但对峰值冲击力增加了阈值限制,即FPθ-L<120 kN。点阵结构填充吸能盒的抗撞性多目标优化数学模型为
式中:l为正六边形胞元的边长值;
α为正六边形胞元的长度系数,h/l;
β为正六边形胞元的厚度系数,t/l;
γ为正六边形胞元的胞元夹角;
T为本体的厚度。这里需要说明的是:当结构参数进行变化时,会对本体结构的截面进行适当微调,以实现点阵结构与壳体之间的装配。
4.2.2 样本点确定和代理模型的精度评估
采用最优拉丁超立方法进行47组样本点的筛选,前42 组用于构建代理模型,后5 组用于验证模型精度。表6给出不同样本点及其对应的目标性能值。

表6 不同样本点及其对应的目标性能值
基于前42 组样本点,采用响应面法对代理模型进行构建如下:
采用后5 组样本点对上述3 个代理模型进行精度验证,如表7 所示。可以观察到:所有样本点的仿真值与预测值的误差均在10%以内。进一步采用平方误差R2、均方根误差RMSE、相对平均绝对误差RAAE和相对最大绝对误差RMAE进行代理模型的评估[13],如表8 所示。可以看到R2值均接近于1,其他3个指标均接近于0,因此认为代理模型具有可信的精度,可以用于后续的多目标优化分析。

表7 代理模型精度验证

表8 代理模型精度评价指标
4.2.3 多目标优化设计及验证
基于上述代理模型,采用第二代遗传算法进行多目标优化设计,经多次迭代得到pareto 解集,如图9 所示,并采用理想点法获得最终优化解(图中绿点),即l=9.87 mm,α=0.143,β=0.775,γ=39.29°,T=2.998 mm,FPθ-L=113.75 kN,Favθ-L=62.36 kN,SEAθ-M=16062 J/kg。

图9 pareto解集与最优解
为验证优化结果的准确性,对该优化解进行仿真计算,获得实际的性能值为:FPθ-L=111.4 kN,Favθ-L=61.19 kN,SEAθ-M=15839 J/kg,其与预测值的误差分别为2.11%、1.91%、1.41%,均在误差范围内,因此认为优化值有效。进一步地,对优化前后的性能改进效果进行对比,如表9所示。
从表9 可以看出:优化后的点阵结构填充式吸能盒在质量方面相对于本体结构有所增加,但其与第3 节最初的吸能盒壳体结构的质量1.149 kg 相比,仍有32.05%的减质量效果。在峰值冲击力方面,点阵结构填充式吸能盒由于内芯结构的引入使最大反力上升,但小于预先设置的阈值120 kN。在平均压溃力方面,点阵结构填充式吸能盒具有45.30%的提升效果,这将大大增强低速工况下的抗撞性能。在综合比吸能方面,点阵结构填充式吸能盒相对于本体结构改善了15.17%,使中速冲击工况下的单位质量吸能量得到进一步增强。同时,优化后的结构在吸能稳定性方面具有大幅提升,意味着吸能盒结构具有更好的冲击角度适应性,在各冲击工况下均能展现出优异的吸能性。以上优化结果充分验证了本体结构的改进设计对角度冲击下性能提升效果的重要影响。

表9 优化前后的目标性能对比
对比研究了不同点阵结构填充吸能盒在多角度冲击工况下的综合耐撞性能,对点阵结构填充吸能盒的吸能影响机制进行分析,进一步阐述了点阵结构内芯的选择依据。区别于现有研究集中对内芯结构进行设计,本文重点关注本体结构对综合耐撞性能的影响,开展了基于改进本体结构的点阵结构填充式汽车吸能盒抗撞性多目标优化设计,得到主要结论如下。
(1)通过分析不同点阵结构填充吸能盒的综合耐撞性能,发现正泊松比点阵结构填充吸能盒具有更加优异和稳定的吸能能力。
(2)轴向冲击工况下,正泊松比点阵结构填充内芯有利于促进内芯与本体结构的相互作用,吸能效率得到显著增强;
负泊松比点阵结构填充内芯由于其独特的压缩收缩特性,其具有较低的峰值冲击力,但一定程度上减弱了相互作用。斜向冲击工况下,点阵结构填充吸能盒呈现出更加明显的耦合效应。
(3)考虑本体结构对点阵结构填充吸能盒性能提升效果的影响,基于改进本体结构的点阵结构填充式汽车吸能盒进行抗撞性多目标优化设计。相比于传统吸能盒,优化方案具有32.05%的减质量效果,且在吸能稳定性方面具有大幅提升,意味着吸能盒结构具有更好的冲击角度适应性,在各冲击工况下均能展现出优异的吸能性,充分验证了本体结构的改进设计对角度冲击下性能提升效果的重要影响。
猜你喜欢内芯泊松比六边形知识快餐店 到处都是六边形小哥白尼(趣味科学)(2021年6期)2021-11-02具有负泊松比效应的纱线研发纺织科技进展(2021年8期)2021-09-01负泊松比功能的结构复合纺纱技术进展毛纺科技(2020年6期)2021-01-06考虑粘弹性泊松比的固体推进剂蠕变型本构模型①固体火箭技术(2019年4期)2019-09-13固体推进剂粘弹性泊松比应变率-温度等效关系固体火箭技术(2019年3期)2019-07-31创意六边形无限翻童话世界(2018年32期)2018-12-03怎样剪拼学生导报·高中版(2017年23期)2017-09-10怎样剪拼学生导报·初中版(2017年23期)2017-09-10不一样的/i?/和/I/小学生时代·大嘴英语(2017年3期)2017-04-11人教版八上第四单元写作·使用恰当的说明方法作文新天地(初中版)(2016年12期)2017-01-05